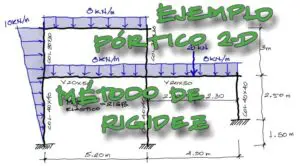
Planteamiento del problema

Se plantea resolver el siguiente problema mediante el método de rigidez o también llamado método matricial.

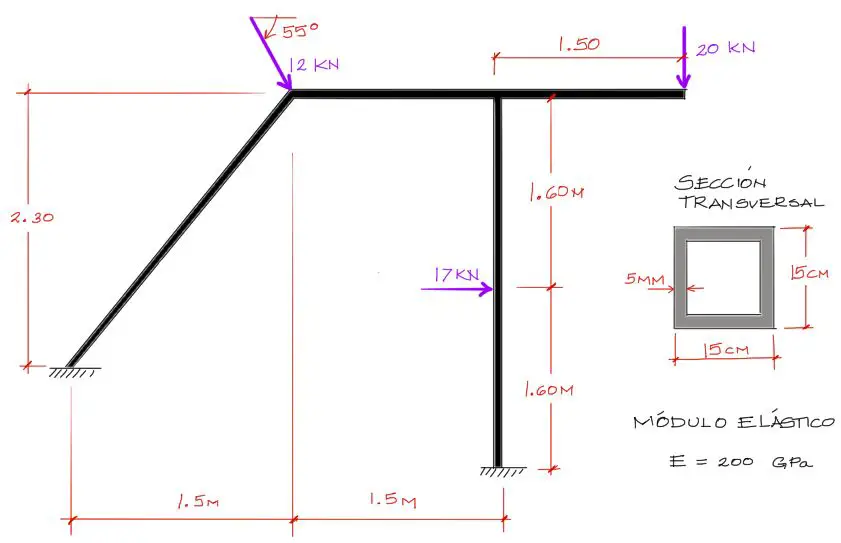
Las características del problema denotan lo siguiente:

• El pórtico es hiperestático
• Existen elementos de pórtico inclinados
• Solo existen cargas puntuales en el enunciado
• Las secciones transversales son constantes

Solución

Paso 1) Numeración de nudos, grados de libertad y barras

En este proceso es conveniente ir de izquierda a derecha en la numeración de todos los elementos mencionados.

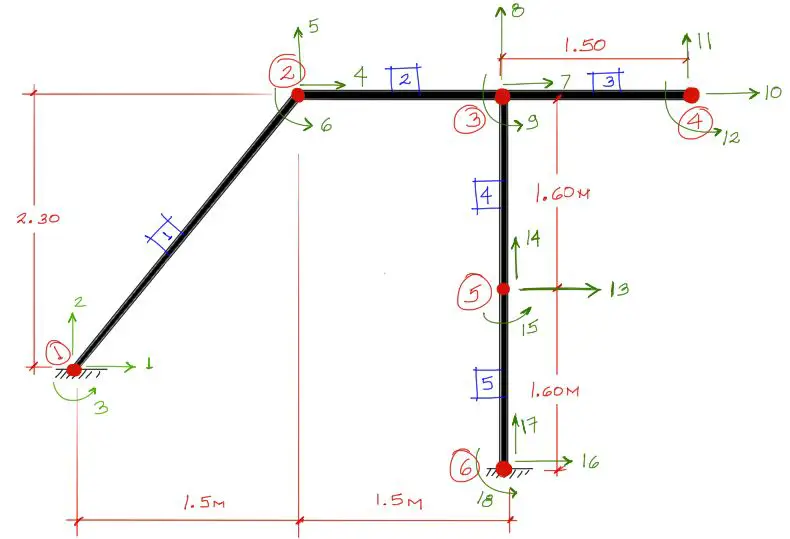
Para la numeración de grados de libertad debe notarse que cada nudo consta de tres grados de libertad: Desplazamiento en X, Desplazamiento en Y, Giro.

Paso 2) Datos de cada barra

Los datos necesarios de cada barra para ingresarlos a la matriz de rigidez de cada elemento son:

• Longitud
• Inclincación
• Módulo elástico
• Sección transversal (área)
• Inercia

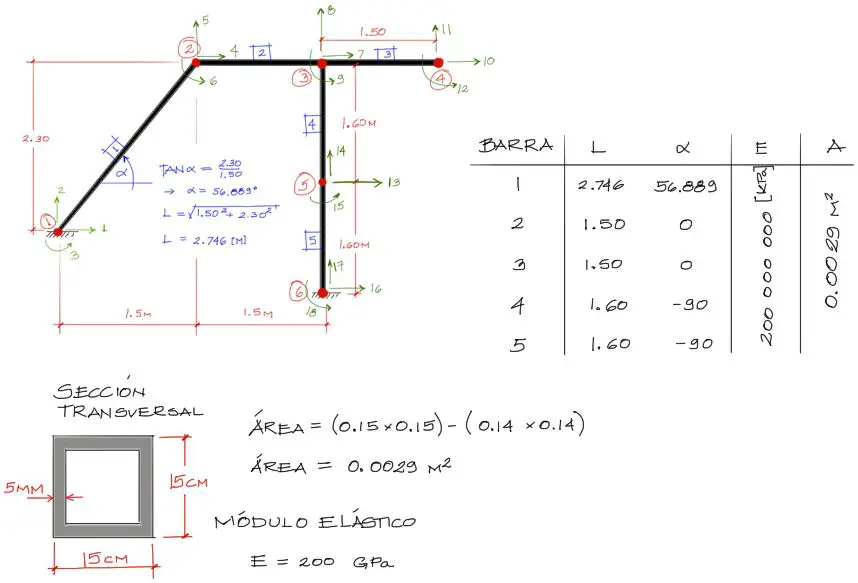
En ese contexto se deben realizar algunos cálculos previos para encontrar los datos necesarios. Los aspectos a tomar en cuenta son los siguientes:

• El ángulo de inclinación debe medirse SIEMPRE desde el eje positivo X, acomodando el nudo de menor numeración en el eje de coordenadas.
• La sección transversal de las barras deben obtenerse en m², ya que las cargas están en S.I.
• La inercia debe obtenerse en m4, por el mismo motivo anterior
• El módulo elástico debe calcularse en KPa, ya que las cargas están en KN

Con esas consideraciones, se tiene lo siguiente:

Paso 3) Se calcula la matriz de rigidez [Ke] de cada elemento

Para calcular la matriz de rigidez de cada elemento se deberá aplicar la fórmula ya deducida en la publicación de Teoría de matríz de rigidez de pórticos. La matriz de rigidez deducida allí, se la muestra a continuación:

Toma en cuenta de esta matriz, que c=cos(α) y s=seno(α). El resultado de la multiplicación de estas tres matrices será la matriz de rigidez del elemento, en coordenadas globales.

Calculando entonces cada uno de los elementos en base a la tabla resumen de datos de cada barra y la matriz de rigidez de la última imagen, calculamos:

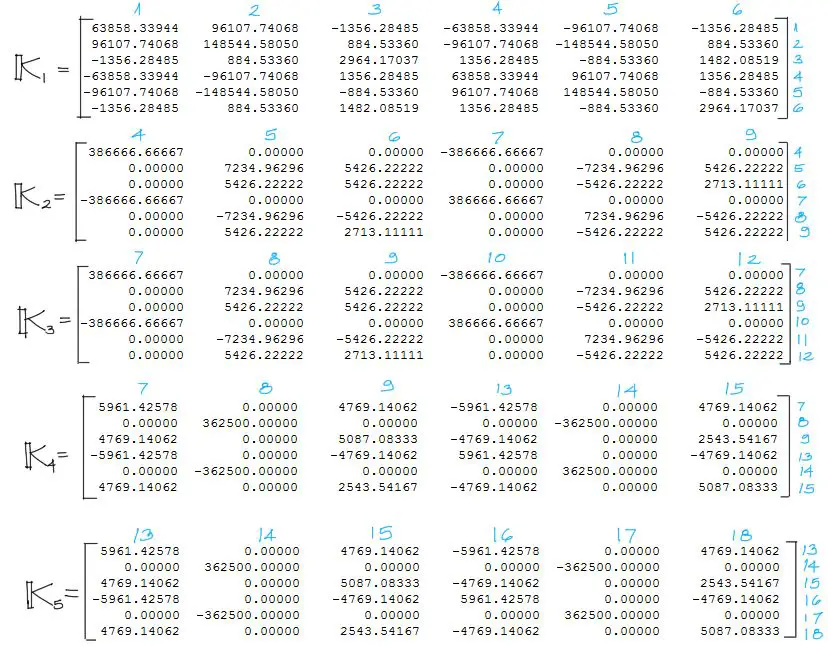
Un aspecto a tomar en cuenta es la numeración en celeste de cada matriz de rigidez elemental. Estos números corresponden a los grados de libertad de cada barra. La numeración de los grados de libertad para cada matriz elemental debe anotarse desde el menor grado de libertad de esa barra hasta el mayor. Por ejemplo la barra 4 arranca en el nudo 3 (nudo de menor numeración) con grados de libertad 7 8 9 y termina en el nudo 5 (nudo con mayor numeración) con grados de libertad 13 14 15. Estos valores van anotados como índices en la matriz de rigidez de este elemento.

Paso 4) Ensamblaje de la matriz de rigidez global [Kg]

Para ensamblar las matrices de rigidez elementales dentro de la matriz de rigidez global se debe tomar en cuenta los siguientes pasos:

• Crear una matriz de ceros con dimensión cuadrada igual al número de grados de libertad del sistema (en este caso 18×18)
• Trasladar cada elemento de las matrices de rigidez elemental a la global según los índices en celeste anotados arriba y a la izquierda. Estos índices corresponden a la posición de estos elementos en la matriz de rigidez global.
• Si en el proceso anterior, dos valores cayeran dentro de la misma casilla en la matriz de rigidez global, estos valores deben sumarse.

Con todas las consideraciones necesarias mencionadas arriba, se obtiene entonces la matriz de rigidez siguiente:

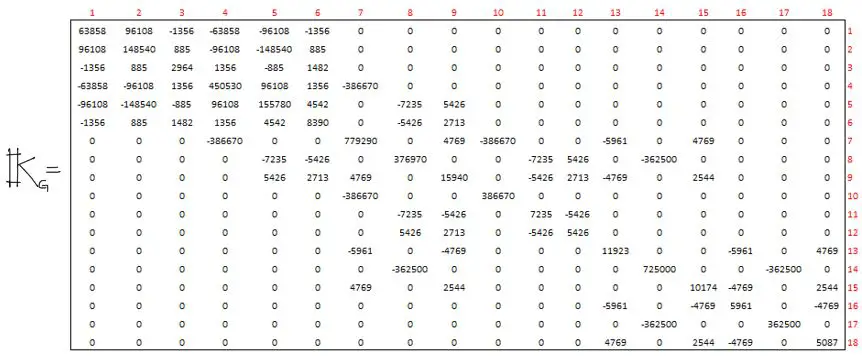
Paso 5) Sistema de ecuaciones y condiciones de contorno

Ensamblada la matriz de rigidez, se arma el sistema de ecuaciones a resolver siguiente:

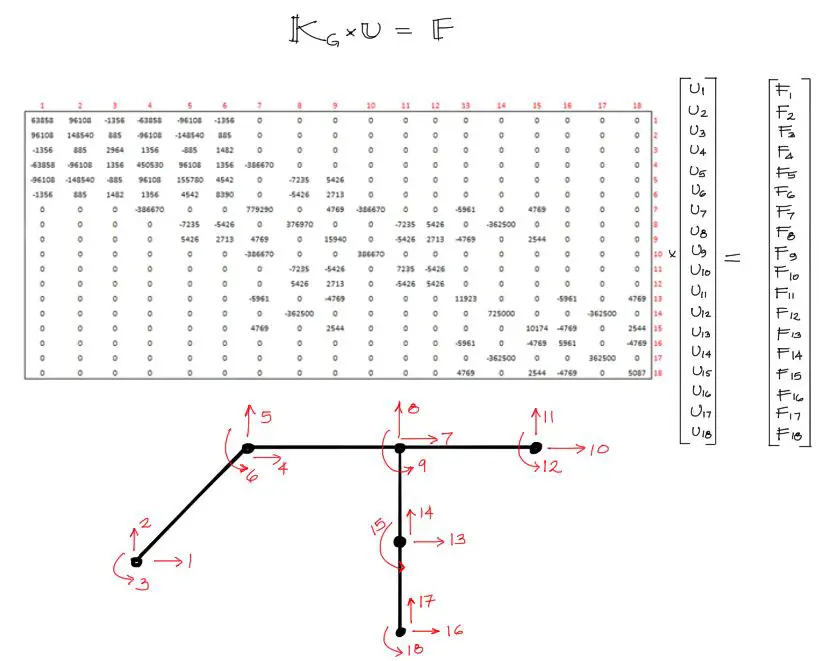
Al sistema de ecuaciones lo acompaña un esquema de la estructura con los grados de libertad mostrados, ya que a partir de acá se impondrán las condiciones de contorno al sistema de ecuaciones.

Si dibujamos las incógnitas de equilibrio externo de la estructura y sus cargas, se tiene lo siguiente:

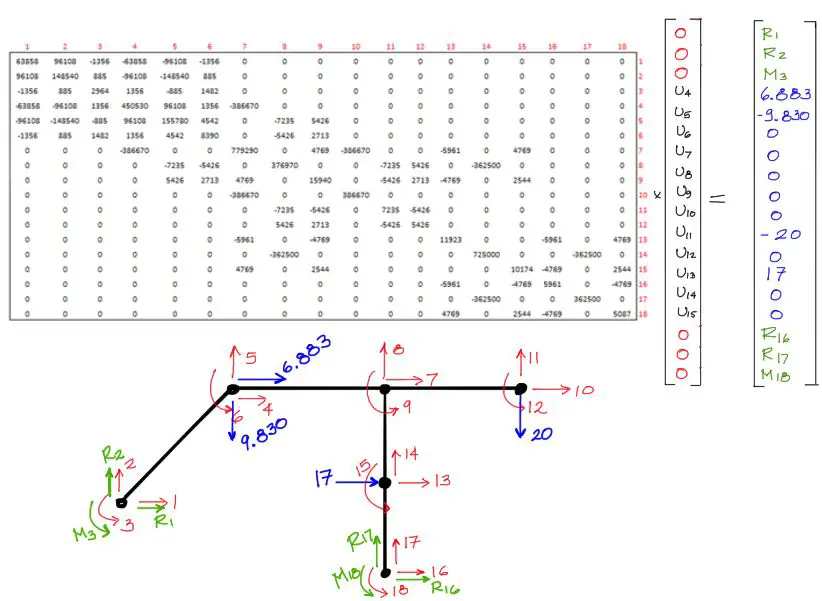
De la imagen con las fuerzas y reacciones mostradas, podemos comenzar a imponer las condiciones de contorno al sistema de ecuaciones. Para eso seguimos los siguientes pasos:

• Donde exista apoyo (restricción de desplazamiento o giro) ese grado de libertad será igual a cero.
• Donde no exista carga ni restricción (apoyo), la fuerza será igual a cero
• Donde exista apoyo, para ese grado de libertad existirá siempre una reacción
• Donde se conocen los desplazamientos, las fuerzas (o reacciones) son desconocidas
• Donde se desconozcan los desplazamientos, las fuerzas son siempre conocidas

Paso 6) Sistema de ecuaciones reducido

Una vez que se hayan impuesto todas las condiciones de contorno en el sistema de ecuaciones se deben anular las filas y columnas de los grados de libertad restringidos, o sea los grados de libertad cuyos desplazamientos sean iguales a cero. La siguiente figura muestra este proceso

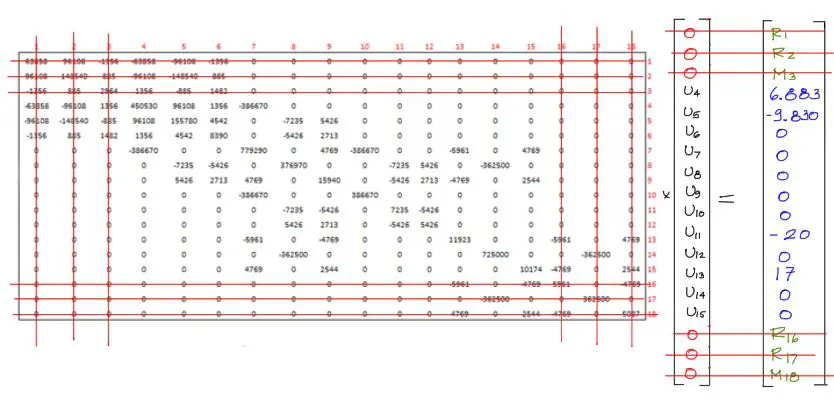
Se conforma entonces un sistema de ecuaciones reducido donde todas las incógnitas están al lado izquierdo del sistema de ecuaciones y todo las fuerzas conocidas están al lado derecho, y de esta manera se puede resolver el sistema de ecuaciones.

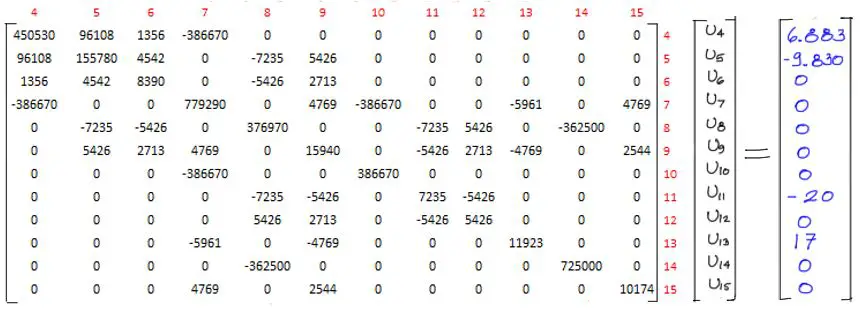
Paso 7) Resolución del sistema de ecuaciones

No es recomendable utilizar una resolución invirtiendo la matriz cuadrada pues esto genera errores numéricos que pueden no ser convenientes y además el uso de procesador es muy alto.

Es mejor aplicar métodos numéricos especializados para la resolución de sistemas de ecuaciones como por ejemplo el método de Gauss Jordan.

Realizando Entonces esta resolución nos quedan los siguientes resultados de desplazamientos:

Paso 8) Reacciones en la estructura

Una vez conocidos los desplazamientos del paso anterior se pueden encontrar las reacciones del sistema reemplazando los desplazamientos conocidos en el sistema de ecuaciones original antes de ser reducido, como se muestra en la imagen:

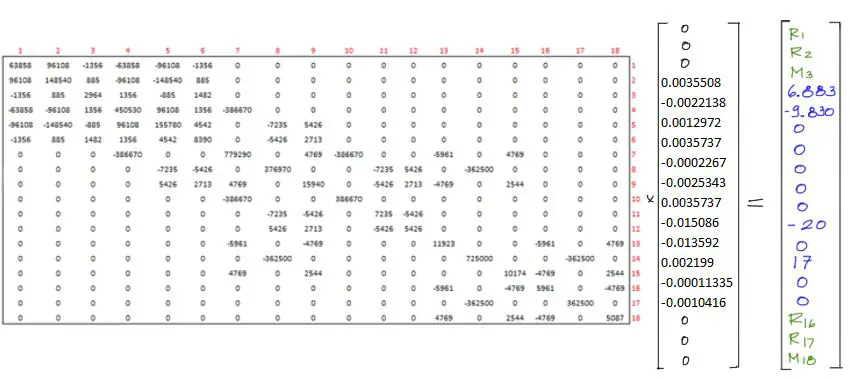
Hecho esto se multiplica la matriz cuadrada de 18×18 por el vector de desplazamientos de 18×1 quedando la igualdad mostrada en la siguiente imagen. En la imagen a continuación se puede ver una igualdad de dos vectores de donde sólo nos sirve rescatar las posiciones 1 2 3 16 17 y 18. Las demás posiciones desde la fila 4 hasta la fila 15 Simplemente nos van a dar una identidad que corrobora que el sistema ha sido bien resuelto.

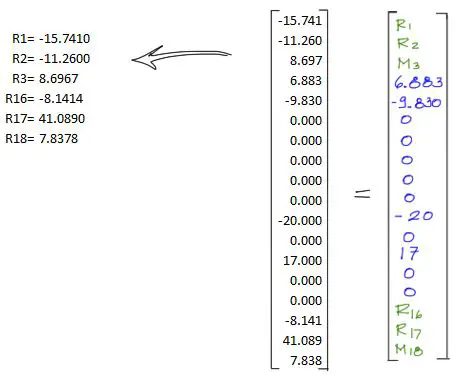
La estructura entonces queda con las reacciones de la siguiente manera

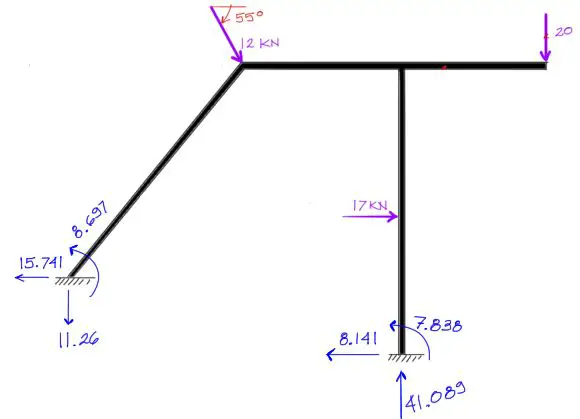
Paso 9) Postproceso

A partir de este momento queda calcular las solicitaciones internas de las vigas y columnas de la estructura mediante teoría de la elasticidad, que no se analizará en esta publicación sino en la siguiente publicación:

Ejemplo de resolución de pórtico con cargas puntuales – 2da Parte

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS←←←