
Enunciado
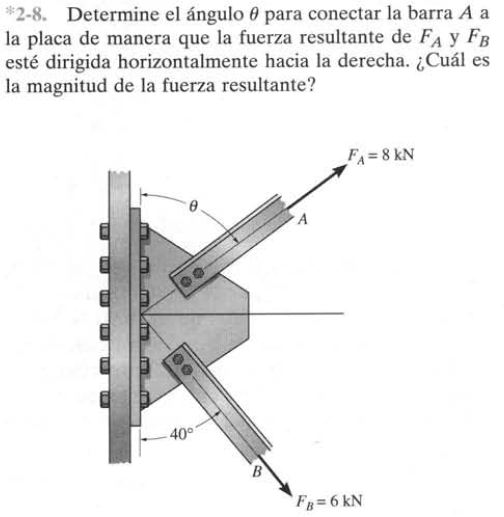
Resolución
Para la resolución de este ejercicio debemos escribir los dos vectores de fuerza Fa y Fb en función de sus componentes.
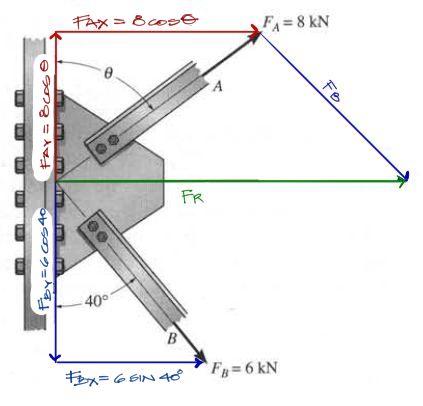
Como la fuerza A está en función de un ángulo desconocido, escribimos las componentes de Fa en función a este ángulo:

Luego, este es un ejercicio de resultante de fuerzas, y el enunciado indica que se debe encontrar un ángulo θ tal, que genere un vector resultante horizontal. Esto quiere decir que debe generarse un vector horizontal que sólo tenga componente en X, y su componente en Y sea cero.
Por tanto el vector resultante será:
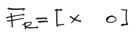
Luego se suman las componentes de las fuerzas Fa + Fb = Fr, quedando:

Se resuelve el sistema despejando θ de la segunda ecuación, y reemplazandola en la primera. De esta forma se encuentran θ y X

Finalmente, se tiene la respuesta de las componentes del vector Fr, cuyo módulo es 10.404 kN. Con esto termina el ejercicio
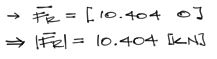
Vídeo
La explicación en vídeo la puedes ver a continuación
autor: Marcelo Pardo


excelente explicacion
Muchas gracias Guillermo!
Me gusta la explicacion