Introducción

Esta ya se trata de una materia de tercer o cuarto año de la carrera de ingeniería civil, del área de estructuras

Concretamente, necesitas conocimientos de resolución de cerchas o de vigas por métodos de Rigidez o también conocidos como métodos matriciales para entender esta publicación.

Lo que pretendo mostrar en esta publicación en concreto es la demostración de la matriz de rigidez de un pórtico en coordenadas globales

Matriz de rigidez de pórtico en coordenadas locales

Los elementos de pórtico en 2D no son otra cosa que una combinación de dos tipos de elementos:

• a) Elementos con deformación axial
• b) Elementos de viga.

Los elementos de cercha, como se vio anteriormente, para los grados de libertad mostrados tiene la siguiente matriz de rigidez local.

A la vez, vimos que los elementos de viga tienen la siguiente matriz de rigidez:

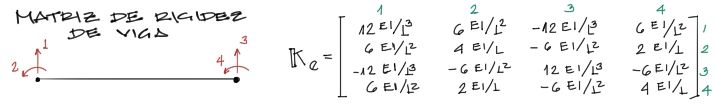
Si combinamos ambos efectos en un elemento de barra que contenga tanto deformaciones axiales, verticales y giros en los nudos, sobreponiendo efectos de los dos anteriores, se tiene:

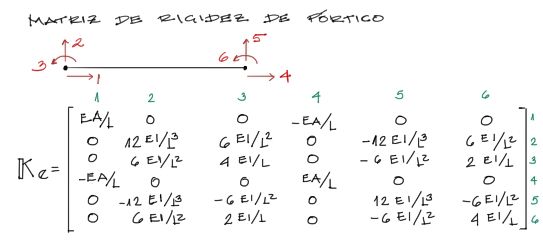
… donde se han re enumerado los grados de libertad desde el 1 hasta el 6 para combinar ambos efectos.

Como se puede ver en la última imagen, la última matriz consiste en la matriz de rigidez de un elemento de pórtico en coordenadas locales. Se combinaron ambos efectos tanto de deformación axial como de deformación transversal para conformar un elemento cuyos nudos se trasladen en x,y y roten.

Esta matriz de rigidez multiplicada por los desplazamientos es igual al vector de fuerzas y reacciones del elemento en coordenadas locales. Ésta es la conocida fórmula del sistema de ecuaciones a resolver por elementos finitos:

(ecuación 1)

Matriz de transformación de coordenadas

Para poder rotar este elemento de pórtico a cualquier dirección se necesitan utilizar matrices de rotación. Entonces deberemos poder convertir los desplazamientos y fuerzas de coordenadas locales a coordenadas globales.

Para lograrlo debemos concebir ambos sistemas como se muestra en la siguiente figura:

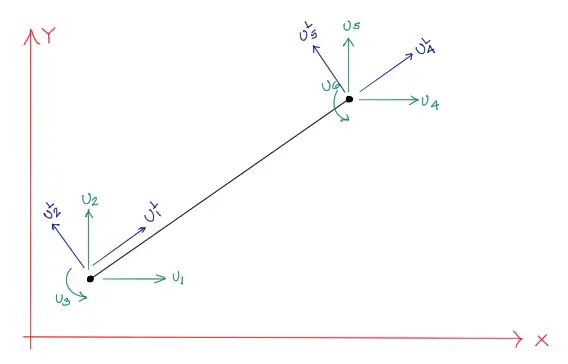
si queremos convertir por ejemplo el desplazamiento U1 local al sistema global debemos expresar U1 local como:

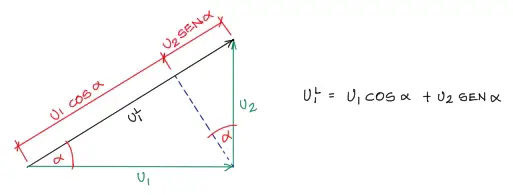
Debemos proceder de la misma manera con los grados de libertad U2, U4, U5 locales. Los grados de libertad U3 y U6 no necesitan transformación pues corresponden a giros.

Terminado el proceso de transformación y escribiendo las ecuaciones en sistema matricial se obtiene la siguiente matriz de transformación:

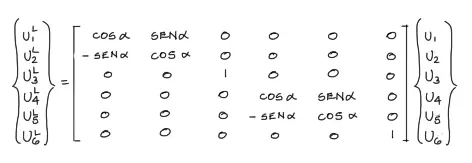
Donde a esta última matriz de senos y cosenos de 6×6 llamaremos matriz de transformación [T]

Matriz de rigidez de pórtico en coordenadas globales

Tanto para los desplazamientos como para las fuerzas, podemos escribir los vectores locales en función de los globales de la siguiente manera:

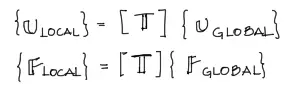
Y reemplazando {U local} dentro del sistema de ecuaciones 1 que lo volvemos a mostrar a continuación,

, se tiene:

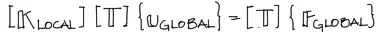
Si multiplicamos toda esta última ecuación por la inversa de [T] a ambos lados, se anula el término [T] del lado derecho de la ecuación, y debido a que para matrices ortogonales como lo es la matriz [T], la inversa es igual a la transpuesta, finalmente se tiene el sistema de ecuaciones final:

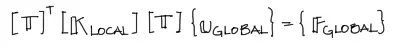
donde la matriz de rigidez en coordenadas globales es:

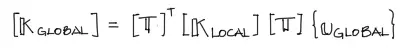
Desglozando esta matriz en todas sus componentes se tiene:

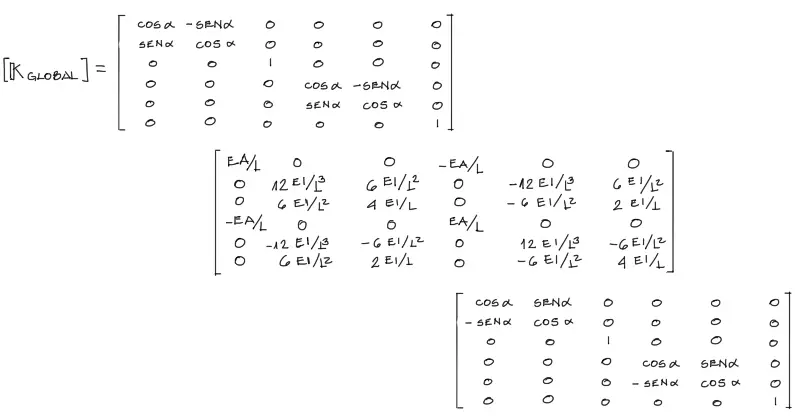
Ésta última es la matriz de rigidez en coordenadas globales para elementos de pórtico en 2 dimensiones.

Con esta matriz resultante de 6×6 elementos se tienen por tanto todos los datos físico mecánicos de un solo elemento de pórtico, que deberá ensamblarse con todos los otros elementos de pórtico de la estructura para obtener la matriz de rigidez global de toda la estructura y posteriormente resolver los desplazamientos.

Ejemplo

El siguiente paso para entender el uso de esta matriz es mediante un ejemplo completo. Se sugiere el siguiente ejemplo con cargas puntuales en los nudos como primer ejemplo de aprendizaje de cálculo de pórticos por el método de rigidez:

– Ejemplo de pórtico con cargas puntuales – 1ra parte
– Ejemplo de pórtico con cargas puntuales – 2da parte

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS←←←