El problema completo
Generalmente los problemas de estructuras se presentan de la siguiente manera:
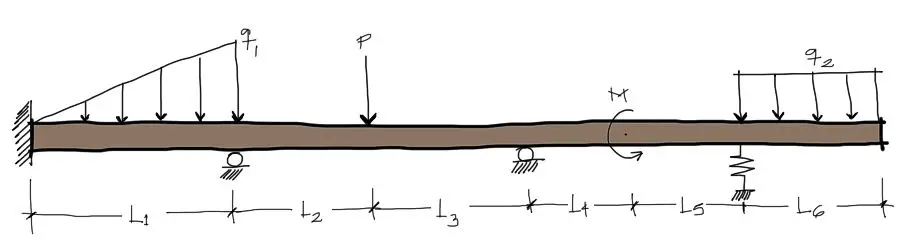
Cuando necesitamos resolver un problema de vigas por el método de rigidez, debemos dividir la viga arriba en varias partes de longitud finita. Estas divisiones deberán localizarse en puntos donde exista:
- Un cambio en el tipo de carga distribuida
- Comienzo o fin de carga distribuida
- Una carga puntual
- Un momento de Par
- Un apoyo movil, fijo o empotrado
- Un resorte
- Un extremo de voladizo
La matriz de rigidez
Cada uno de los tramos divididos, denotados por las longitudes L1, L2, L3, etc, tendrá propiedades que estarán en base a su longitud L, su módulo de elasticidad E, e inercia I. Además cada uno de estos tramos tendrá en los extremos un nudo con dos grados de libertad.
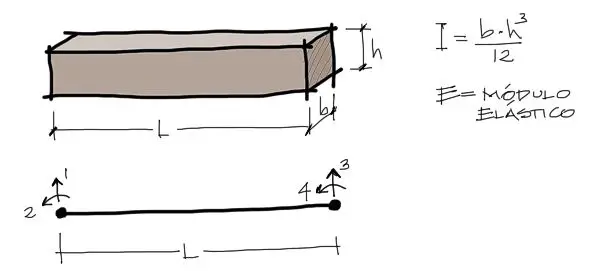
Todas estas propiedades se condensan en una MATRIZ DE RIGIDEZ cuadrada que relaciona los desplazamientos del tramo con las fuerzas externas de ese tramo de viga.
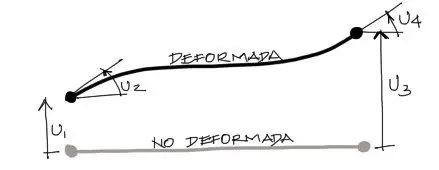

Arriba se ven los desplazamientos y giros del tramo de viga. U1 y U3 denotan los desplazamientos verticales (digamos en metros). U2 y U4 representan los giros del tramo de la viga en radianes. La matriz de rigidez cuadrada con las propiedades de E,I,L multiplicada por estos desplazamientos da como resultado las fuerzas en los extremos de la viga siguientes:

De toda la fórmula de arriba, la mayoría de las veces se maneja la matriz de rigidez suelta para luego ensamblarla dentro de una matriz de rigidez global que represente la relación de deformaciones y fuezas externas y cargas en toda la estructura.

autor: Marcelo Pardo


excelente aporte ingeniero
muchas gracias ingeniero!
Muchas gracias Diego!!!