El método
Cuando calculamos vigas por el método de rigidez asumimos que la viga es contínua de extremo a extremo, y por tanto existe continuidad en pendiente y deflexión en los nudos entre elementos.
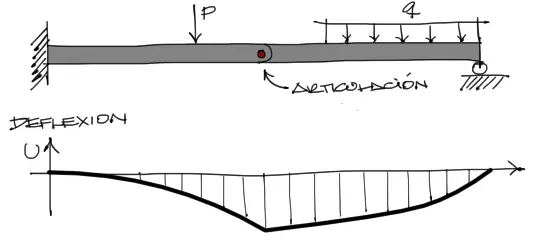
Sin embargo cuando introducimos una articulación en algún punto de la viga, la continuidad de esta deflexión se pierde, formandose un quiebre en la forma de la deflexión de la viga, y además reconfigurando todo el sistema de solicitaciones internas de la viga.
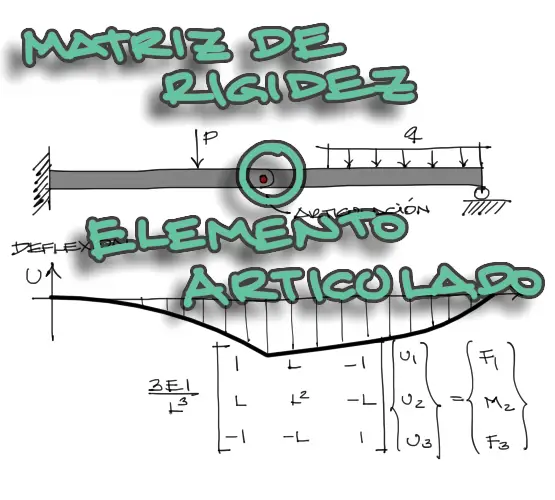
En una anterior publicación de Matriz de rigidez de viga, había mencionado que la matriz de rigidez tiene la forma siguiente:

Esta matriz de rigidez solo sirve para vigas contínuas que no tienen rótulas intermedias. Si se quiere introducir una rótula o articulación en el centro de la viga,se debe modificar esta matriz de rigidez.
Introduciendo una articulación al extremo derecho de la barra
Comenzaremos por el sistema de ecuaciones de un elemento finito con sus respectivos desplazamientos y fuerzas externas:

imaginemos que deseamos generar una articulación que libere la resistencia a flexión en el nudo derecho del elemento. En este caso, el elemento solo resistirá con 3 grados de libertad:
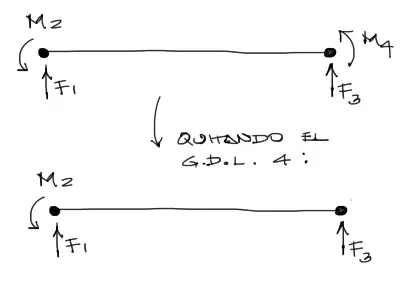
En este momento el elemento ya no resiste momentos flectores en el nudo derecho. Matemáticamente se debe igualar a cero el momento M4, y redistribuir los giros “u4” entre los otros desplazamientos, de la siguiente manera. Reescribimos el sistema de ecuaciones sin la notación matricial:
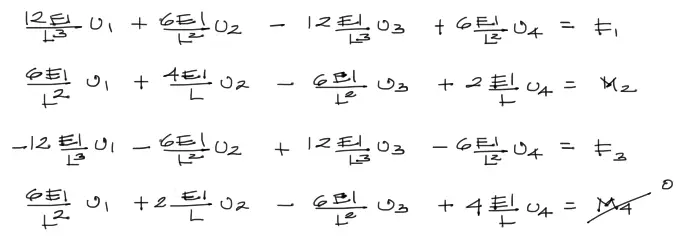
De la última ecuación despejamos u4:

Reemplazamos u4 en las otras tres primeras ecuaciones. Comenzando por la primera:

repitiendo el procedimiendo para las otras 2 ecuaciones, queda:

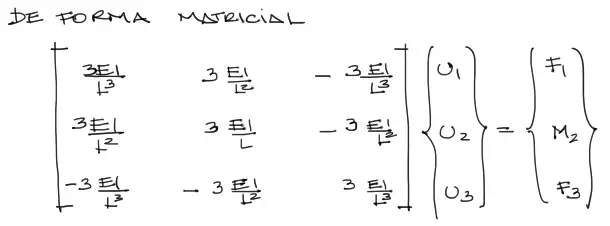
Quedan solo 3 ecuaciones en función de 3 grados de libertad. Matricialmente se reescribe el sistema anterior como:
Podemos reducir un poco la notación anterior, factorizando EI/L³, y queda:
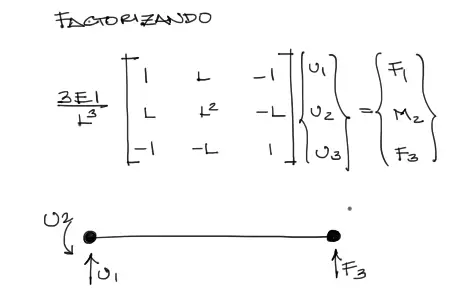
Esta es la matriz de rigidez de un elemento articulado a momento flector a la derecha.
Introduciendo una articulación al extremo izquierdo de una barra
Al igual que en el procedimiento anterior, cuando necesitamos anular el grado de libertad de giro del extremo izquierdo, (grado de libertad 2), anulamos M2, y u2 lo reemplazamos en las ecuaciones 1, 3, 4. El resultado es el siguiente:

Escribiendo el sistema de ecuaciones en forma matricial y factorizando algunos términos, tenemos finalmente:
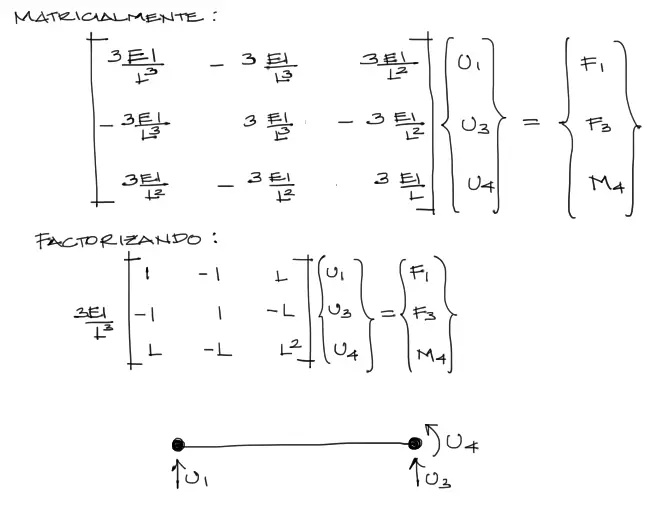
Cuando existe articulación en ambos extremos
Al liberarse los momentos flectores de ambos extremos, el tramo queda inestable y el sistema de ecuaciones formado iguala a cero en el lado izquierdo.
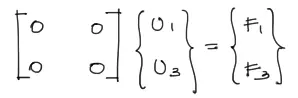
Por tanto si existe un tramo con ambos lados articulados, este servirá para propósitos de cálculo solo como un contenedor de cargas distribuidas que transferirán las cargas equivalentes de los nudos a sus respectivos extremos articulados.
Qué sigue?
Se verificará el uso de las matrices deducidas en un ejemplo posterior
autor: Marcelo Pardo