Resumen de pasos

Los pasos de la resolución de cerchas en 2 Dimensiones puede resumirse en:

1. Definición del problema
2. Numeración de nudos y barras de toda la estructura
3. Longitudes y ángulos de cada barra
4. Matrices de rigidez de cada elemento
5. Ensamblaje de matriz de rigidez de toda la estructura
6. Establecimiento de sistema de ecuaciones
7. Vector de cargas externas puntuales
8. Vector de cargas por peso propio (o distribuidas en general)
9. Vector de reacciones y desplazamientos nulos
10. Anulación de grados de libertad restringidos
11. Resolución del sistema reducido (obtención de desplazamientos)
12. Reacciones del sistema
13. Solicitaciones de cada barra

Cada uno de estos pasos se describe a detalle a continuación

1) Definición del problema

Generalmente los problemas de cerchas en 2 dimensiones provienen de problemas más complejos en 3 dimensiones que pueden simplificarse a un análisis en el plano. Para esto necesitamos idealizar la estructura en elementos articulados en 2 dimensiones con apoyos fijos o móviles.

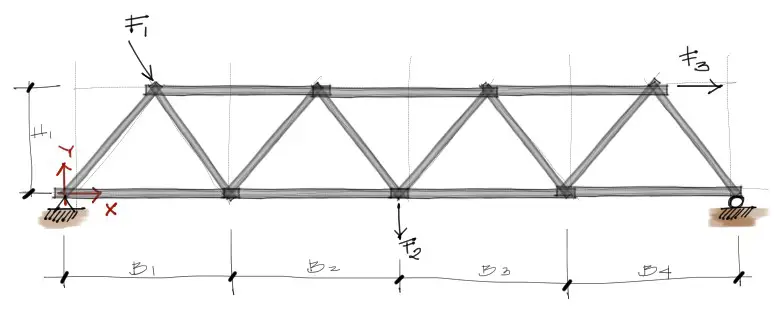
Si las secciones transversales son desconocidas se puede asumir una sección transversal hipotética y un módulo elástico en función al material del cual esté hecha la cercha. En el enlace de módulos elásticos existen valores para diferentes materiales.

Asi mismo, se deben establecer las cargas actuantes sobre la estructura y las distancias entre ejes de todos los nudos.

2) Numeración de nudos y barras de toda la estructura

Establecidos todos los datos de la estructura, se debe imponer una numeración conveniente en los nudos y barras de la estructura. Esta numeración preferentemente debe barrer toda la estructura de abajo hacia arriba y de izquierda a derecha, procurando no volver hacia atrás en el barrido.

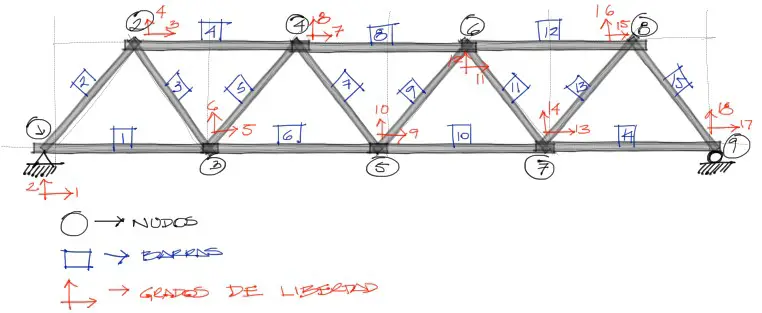
Si bien la sugerencia mencionada arriba sobre el barrido no es obligatoria, es recomendable realizarla de esta manera para tener buen condicionamiento de la matriz de rigidez de toda la estructura.

Con los nudos numerados, se debe además tener presente la numeración de los grados de libertad de cada barra. Los grados de libertad deben tener la misma secuencia y orden que la numeración de los nudos.

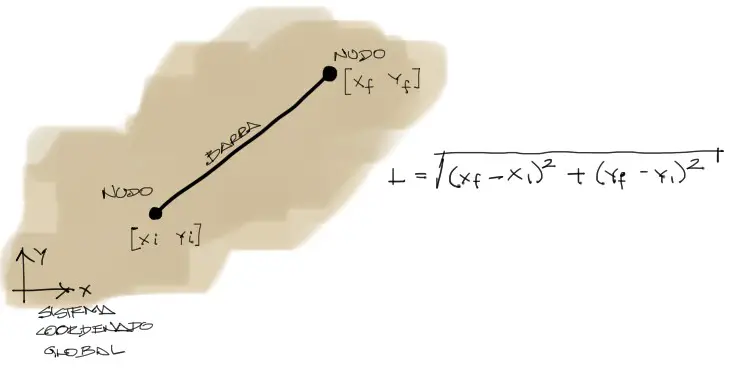
3) Longitudes y ángulos de cada barra

Ya se tienen acá los «nombres» de cada barra, refiriendome a su numeración. El siguiente paso consiste en obtener las longitudes de cada barra a partir de la geometría de la estructura y además el ángulo de dirección de cada barra.

La longitud de las barras se obtiene directamente si la barra tiene posición vertical u horizontal. Sin embargo para barras inclinadas lo mejor es trabajar sobre un sistema coordenado de donde la longitud de cada barra se puede obtener a partir de pitágoras:

Para obtener el ángulo de dirección de cada barra se debe tener presente que el ángulo de dirección de cada barra se calcula siempre medido desde el eje horizontal positivo, en dirección antihoraria positiva u horaria negativa. El eje coordenado local de pivote se debe localizar en el nudo de menor numeración en la barra.

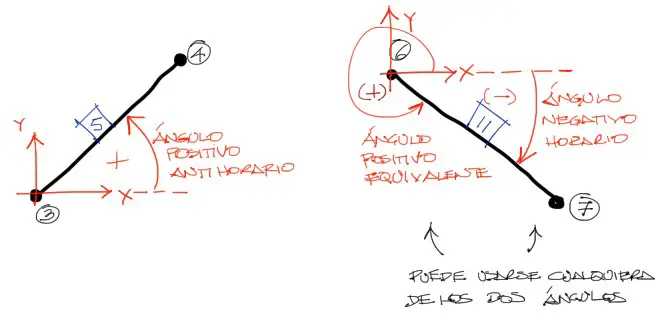
Este es un aspecto que confunde a los que por primera vez aplican el método. Sin embargo es importante recordar que el ángulo medido será positivo en sentido antihorario, para que las fórmulas de transformación de coordenadas de la matriz de rigidez sean válidas.

4) Matrices de rigidez de cada elemento

Con todos los datos de geometría (longitud y ángul) y datos mecánicos (sección transversal y módulo elástico) de cada barra, es momento de calcular la matriz de rigidez de cada barra.

Para esto, se debe simplemente aplicar la fórmula siguiente para cada barra:

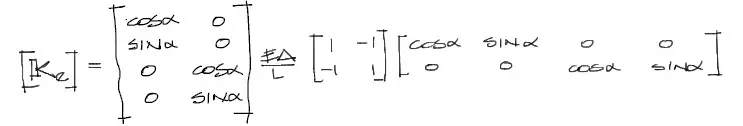
Hechas las multiplicaciones de las tres submatrices que conforman la matriz de rigidez de un elemento, la matriz queda de 4×4 elementos.

Es pertinente denotar con un subíndice a [K] con el número de barra que se está analizando. Este procedimiento debe repetirse tantas veces como barras existan.

A la vez que se van encontrando las matrices de rigidez de cada elemento, se debe establecer la numeración de sus grados de libertad en la parte superior y lateral de cada matriz encontrada. Esta numeración corresponde a los grados de libertad de los nudos a los que está conectada cada barra, comenzando del grado de libertad del nudo con numeración más baja.

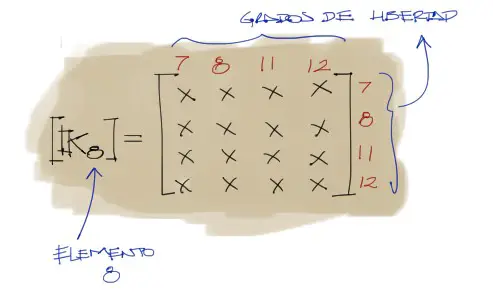
5) Ensamblaje de matriz de rigidez de toda la estructura

Habiendo calculado la matriz de rigidez de cada barra, se debe transportar cada una de estas matrices de rigidez a una matriz de rigidez de toda la estructura.

La matriz de rigidez de toda la estructura, denotada por [K_estructura] tendrá una dimensión igual al total de los grados de libertad de toda la estructura.

Entonces se va transportando cada valor de las matrices de rigidez de cada barra hacia la matriz de rigidez global. La posición dentro de [K_estructura] de cada valor de la matriz de rigidez de cada elemento será la correspondiente a la numeración de los grados de libertad de [K_elemento]:

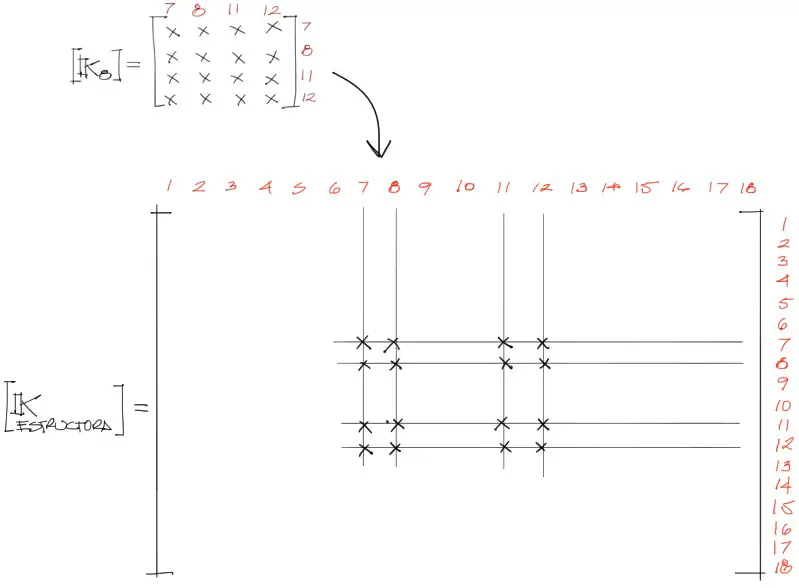
Una manera didáctica de entender este proceso se encuentra en un vídeo que realicé hace años respecto a cómo se realiza un cálculo de este estilo:

Si dos valores numéricos de dos matrices de rigidez de elementos caen dentro de la misma casilla en la matriz de rigidez global, se suman.

6) Establecimiento de sistema de ecuaciones

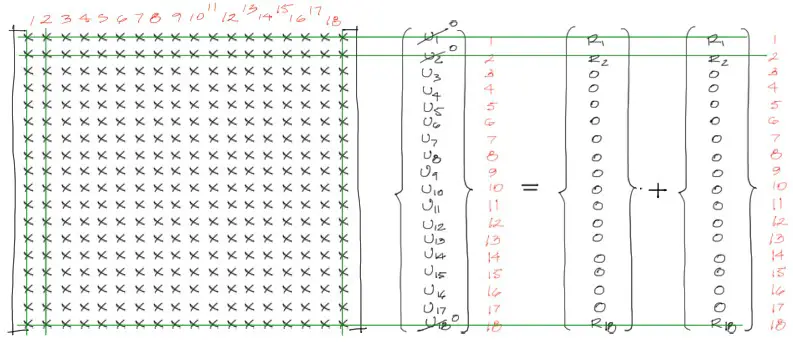
Con la martiz de rigidez ensamblada, se puede ya construir el sistema de ecuaciones que se resolverá donde la matriz de rigidez conforma un sistema de tantas ecuaciones e incógnitas existiran como grados de libertad existan en el sistema. Entonces:

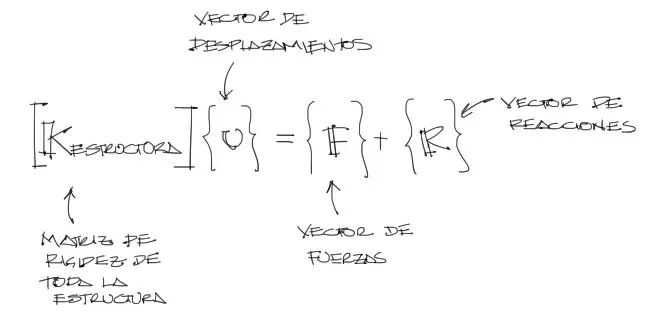
En este sistema de ecuaciones, los desplazamientos «u» son incógnitas del problema en todos los puntos donde los desplazamientos no estén establecidos (tocaré este punto más adelante). El vector de cargas y de reacciones se los explicará a continuación pues aun no están definidos.

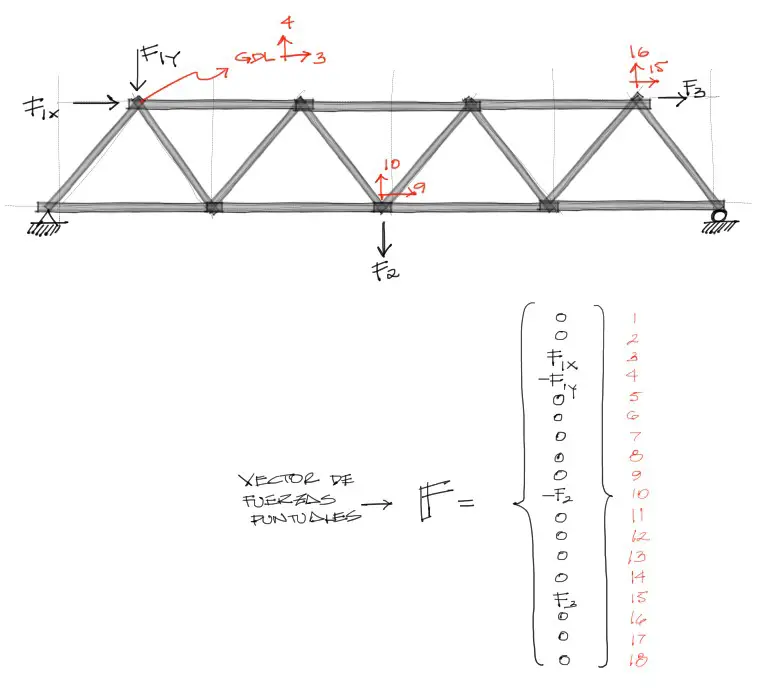
7) Vector de cargas externas puntuales

Para armar el vector de cargas, debe primero concebirse un vector columna vacío que tenga la dimensión de los grados de libertad totales de toda la estructura.

Posteriormente se deben llenar las fuerzas aplicadas en la estructura en este vector. Las fuerzas aplicadas en la estructura deben primero descomponerse en componentes X y Y. Posteriormente se debe determinar en qué grado de libertad está aplicada cada una de estas fuerzas. Se llena la magnitud de cada fuerza en el grado de libertad correspondiente en el vector de cargas.

8) Vector de cargas por peso propio (o distribuidas en general)

Cuando se quiera aplicar una carga distribuida en los elementos de barra, debe convertirse esta carga distribuida en cargas equivalentes en los nudos. El proceso divide la carga distribuida en cargas puntuales iguales en ambos extremos de la barra.

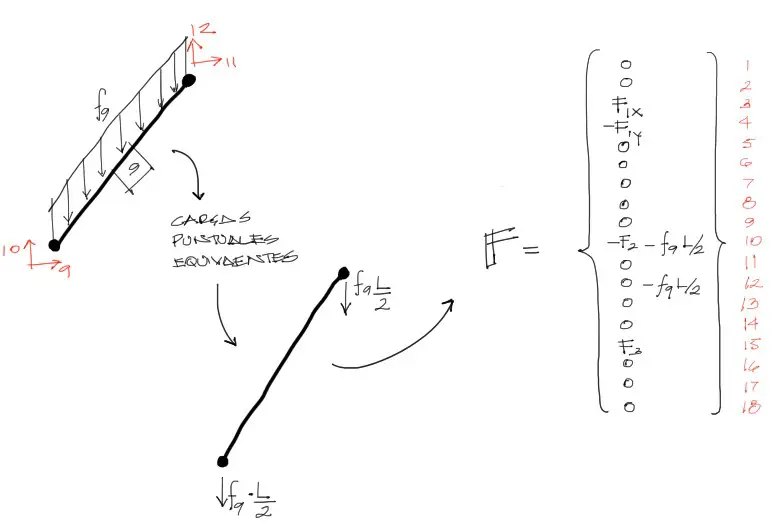
Una vez hecho esto, se debe cargar el nudo con la carga equivalente puntual exactamente de la misma manera como se cargaron las cargas puntuales del anterior subtítulo.

9) Vector de reacciones y desplazamientos nulos

Antes de resolver el sistema de ecuaciones, se debe definir donde los desplazamientos «u» son nulos. Estos desplazamientos serán cero o nulos donde exista una restricción de apoyo. A la vez justo en ese grado de libertad aparecerá una reacción «R» desconocida.

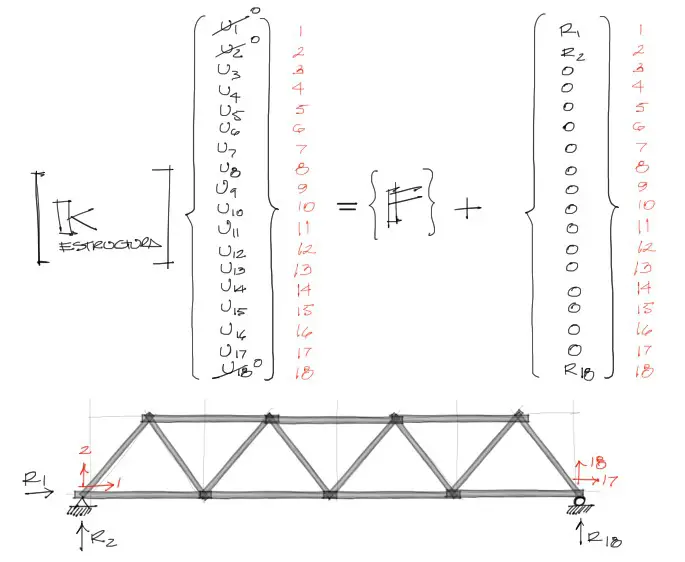
En todos los otros grados de libertad los desplazamientos serán desconocidos o incógnitas, y a la vez las reacciones serán cero.

10) Anulación de grados de libertad restringidos

Hasta este punto ya se tienen todos los elementos del sistema de ecuaciones definidos. El siguiente paso consiste en resolver las incógnitas del sistema de ecuaciones. Lo malo es que existen incógnitas a ambos lados del sistema. Por un lado están los desplazamientos desconocidos de los grados de libertad no restringidos, y en el otro lado de la ecuación existen reacciones desconocidas.

Una manera de resolver el sistema de ecuaciones consiste en anular las filas y columnas del sistema de ecuaciones con los los desplazamientos de los grados de libertad iguales a cero. De esta manera se reduce el sistema de ecuaciones a un sistema del total de grados de libertad de la estructura menos el número de grados de libertad restringidos.

11) Resolución del sistema reducido (obtención de desplazamientos)

Hecha la anulación de filas y columnas, observamos que se han eliminado las reacciones del sistema y además los desplazamientos nulos. Con esto, queda un sistema con puro desplazamientos «u» como incógnitas del sistema. Ahora este sistema de ecuaciones puede resolverse mediante cualquier método conocido de resolución de sistemas lineales de ecuaciones. Por ejemplo Eliminación de Gauss – Jordan.

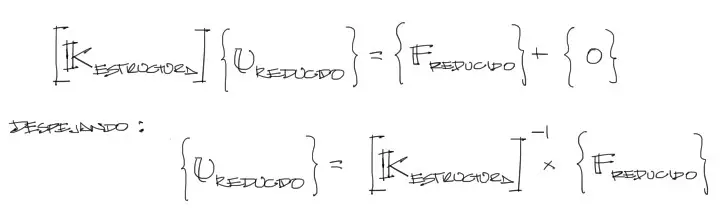
La solución del sistema la escribí como el despeje del vector de desplazamientos. Sin embargo la inversión de la matriz [K] es el procedimiento menos indicado para la resolución del sistema de ecuaciones. Como mencioné antes, es mejor aplicar otro algoritmo como Gauss Jordan para su resolución.

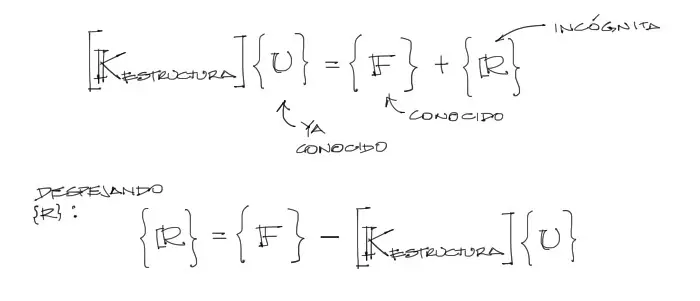
12) Reacciones del sistema

Conocidos ya todos los desplazamientos «u» del sistema, se deben reemplazar los «u» encontrados en el sistema de ecuaciones original antes de reducir y anulas las filas y columnas de los grados de libertad restringidos. A partir de este reemplazo, se despeja esta vez el vector de reacciones para conocer las mismas.

13) Solicitaciones de cada barra

El último paso consiste en encontrar las solicitaciones de cada barra. Para lograr esto se debe trabajar con los desplazamientos locales de cada barra.

Los desplazamientos locales de cada barra se encuentra a partir de una transformación de coordenadas de los desplazamientos globales. Para cada barra se debe realizar el siguiente trabajo.

Debemos resumir en un vector 4×1 los desplazamientos de los extremos de cada barra. Estos desplazamientos {u_global} estarán en cordenadas globales.

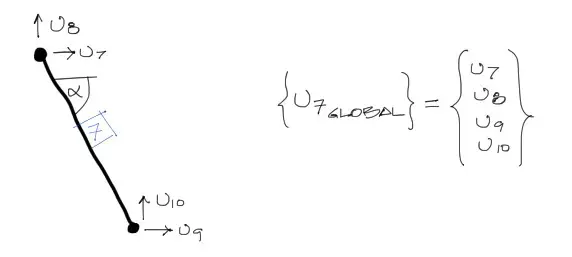
Se deben transformar estos desplazamientos globales al respectivo sistema local de coordenadas de la barra. De esta manera se tendrán solo dos desplazamientos locales por barra.

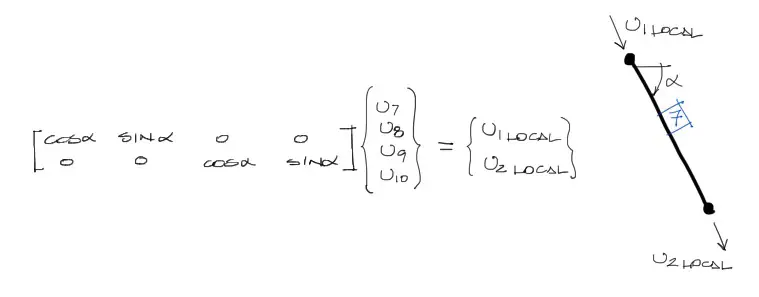
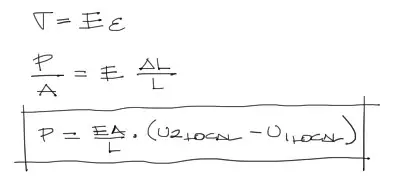
Con estos desplazamientos locales se puede conocer la solicitación axial de la barra en estudio. Se debe repetir este mismo procedimiento para todas las barras. Las solicitaciones obtenidas «P» para cada barra serán positivas si la barra está a tracción y serán negativas para compresión. El signo se obtiene directamente del reemplazo de los valores en la ecuación siguiente:

Ejemplo

Existen dos ejemplos de estructuras pequeñas que cumplen con todos estos pasos, en mi página web:

– 1er ejemplo de cercha en 2D por método Matricial
– 1er Ejemplo de cercha 2D – Continuación – Solicitaciones
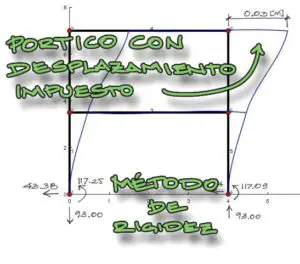
– 2do Ejemplo de Cercha 2D. Desplazamientos, reacciones, solicitaciones

Además, cuento con un tutorial completo de como programar el método en matlab y Octave, en tres vídeos que en total suman 3 horas de explicación respecto a la programación del método.

Espero toda esta información te haya sido útil.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS ←←←