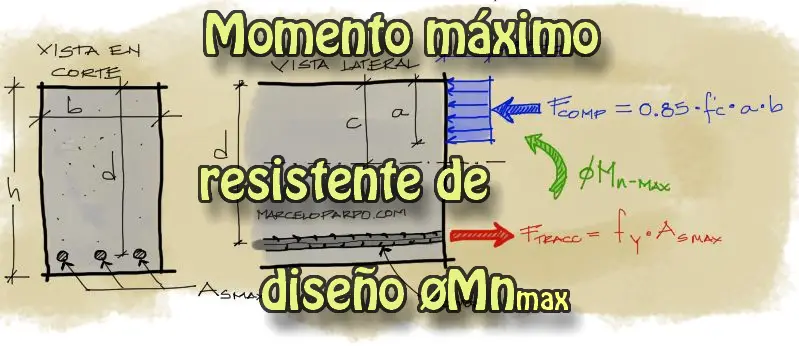
Diferencia entre Mu. øMn y øMn-max

Probablemente a estas alturas de tus estudios de la materia de hormigón armado estés preguntándote sobre todos estos conceptos sin terminar de enternder la diferencia entre cada uno de los términos menciondaos en el subtítulo.

Necesito entonces llevarte por un repaso de todos estos términos antes de explicar qué es el momento máximo resistente de la viga ØMn-max

Momento solicitante “Mu”

El momento solicitante Mu se refiere al momento flector producto de las cargas en las vigas o losas analizadas. Este momento solicitante Mu lleva el subíndice “u” que signifíca “último”.

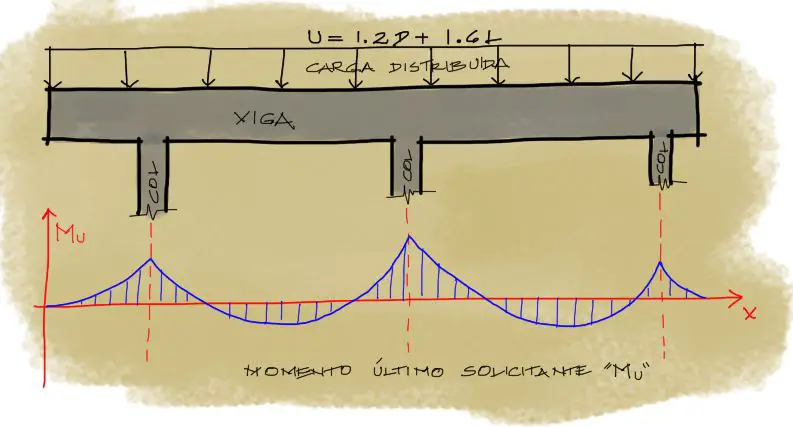
Este momento flector Mu está factorizado (o mayorado) por factores que incrementan las cargas vivas, muertas, de viento, sismo, etc para así obtener momentos flectores mucho mayores a los que solicitarán a la viga en su vida de servicio.

¿Para qué se encuentra este momento mayorado? Para llevar las vigas o losas o elementos estructurales en general a un estado límite o extremo. En otras palabras, para llevar a los elementos estructurales a la falla.

Momento de diseño øMn

Cuando se obtiene el momento último Mu solicitante, se necesita contrastarlo con el momento resistente de la viga. Este momento resistente se denomina momento de diseño “øMn”. Así si Mu es menor a øMn, la viga resiste. Y si por el contrario, Mu es mayor a øMn, la viga fallará.

Este momento de diseño es producto de la multiplicación de un factor de seguridad “ø” por el momento Nominal “Mn”. En vigas ø= 0.90. Además, el “Mn” se puede interpretar como el momento resistente límite de la viga. Si a este momento nominal Mn lo reducimos a un 90%, obtenemos el denominado Momento de diseño.

Este momento de diseño a la vez está muy relacionado a la cantidad de acero de la viga. Entonces a mayor cantidad de acero “As” de la viga, mayor será el momento resistente de diseño.

Momento Máximo de diseño øMn-max

El momento máximo de diseño está completamente ligado al concepto de cuantía balanceada, acero balanceado y acero máximo que puede llevar la viga. Te recomiendo leer el artículo sobre Cuantía balanceada. De esa manera entenderás mejor este concepto.

El Acero máximo (cuyo valor aprenderás a calcular en el artículo de cuantía balanceada) es la cantidad de acero que garantiza que el acero fallará antes que el hormigón. Además, una viga bien diseñada, no deberá superar esta cantidad de acero máximo. Puede imaginarse a As-max como un límite superior de refuerzo de una viga de hormigón armado. Si se sobrepasa, la falla de la viga sería frágil y eso no es bueno. O sea que una viga puede contener una cantidad de acero que fluctue entre una cantidad muy pequeña de acero hasta una cantidad igual a As-max, pero no deberá sobrepasar ésta última.

Luego, el momento máximo de diseño øMn-max se refiere al momento máximo que puede resistir la viga gracias a una cantidad de refuerzo máximo As-max colocada en esta viga. Por encima de este momento máximo øMn-max, la falla de la viga será frágil y no dúctil. Y esto no es bueno.

Deducción del momento máximo de diseño

Para deducir la fórmula del momento de diseño máximo que puede soportar la viga, debemos realizar un corte dentro de la viga y empezar a equilibrar la sección, tanto a fuerzas horizontales como a momentos flectores.

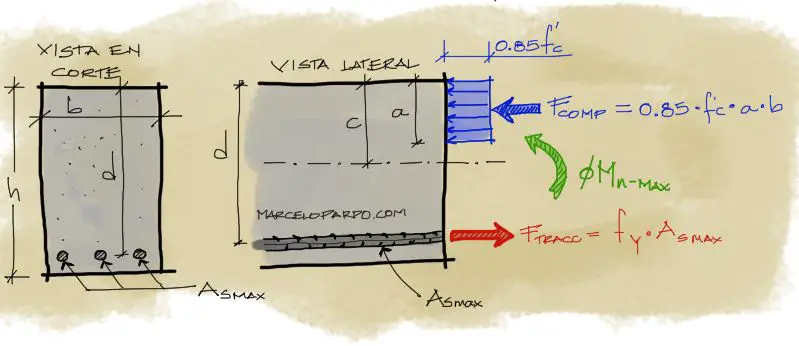
Para estabilizar las fuerzas horizontales, debemos obtener la resultante de fuerzas tanto a compresión como a tracción en la viga. Como ves en el gráfico, el factor de 0.85 que acompaña a f’c se debe a la transformación de esfuerzos del bloque de compresión de una distribución parabólica real a una equivalente rectangular más simple. Luego, la resultante de las fuerzas a compresión es igual al esfuerzo por el área de aplicación del esfuerzo, o sea: Fcomp = 0.85·f’c·a·b

De la misma manera, la resultante de fuerzas a compresión es el esfuerzo resistente del acero (a fluencia) fy por la sección de acero máxima que puede colocarse en la viga. Ftracc = fy·As-max.

Luego realizando el equilibrio, igualamos ambas fuerzas. De la igualación, la única variable desconocida es “a”, que corresponde a la altura del bloque de compresión del concreto. La despejamos entonces.

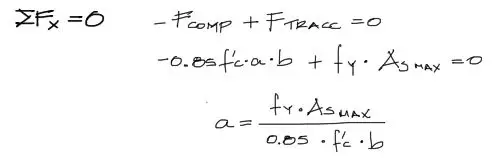
Por otro lado, equilibramos también los momentos de fuerza dentro de la viga. Para esto, a modo de anular una de las fuerzas, podemos hacer pivote de la suma de momentos en el punto donde se aplica la resultante de fuerzas Fcomp. De esta manera la única fuerza que entra dentro de la ecuación es la fuerza de tracción del acero. El brazo de esta fuerza es de (d-a/2) como se muestra en la siguiente figura:

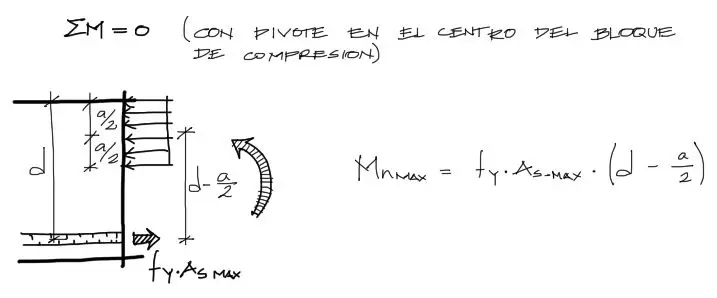
Luego, en esta última ecuación la misma incógnita “a” aparece dentro de la ecuación. Reemplazando “a” desde el despeje de la primera ecuación, reemplazando en la segunda, se tiene:

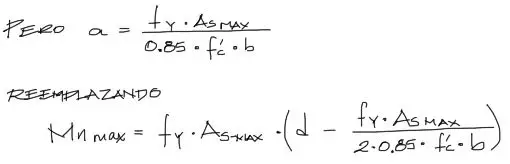
Finalmente, debido a los factores de seguridad que involucran el diseño de vigas según la norma ACI318-14, se castiga esta resistencia nominal máxima a flexión que tiene la viga por el factor Ø que para flexión vale 0.9 y de esta manera se obtiene el momento máximo de diseño que puede resistir la viga.

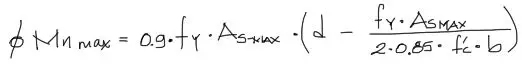
Este resultado obtenido entonces debe ser mayor a cualquiera de los momentos positivos o negativos “Mu” del diagrama de momentos flectores mostrado arriba. En caso de que Mu sea mayor a øMn-max, se debe incrementar la sección de hormigón de la viga ya sea a lo ancho o en altura.

Unidades

Las unidades que deben usarse en esta fórmula son:

• b,d en [m]
• fy, f’c en [MPa]
• As-max en [m²]
• øMn-max en [MN-m]

Excepción a la regla

Existe una alternativa más en caso de que Mu sea mayor a øMn-max, y es la de colocar acero de compresión en la cara de compresión de la viga en la misma medida que se va aumentando el acero de tracción por encima del As-max. Sin embargo esta alternativa trae ciertas dificultades que es mejor comentarlas en una publicación aparte.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE HORMIGÓN ARMADO←←←

→→→ VER TAMBIÉN: DIAGRAMA DE FLUJO DE DISEÑO A FLEXIÓN DE VIGAS DE HORMIGÓN ARMADO →→→