
Pasos previos
Esta es la cuarta publicación de una serie de artículos para resolver un pórtico en 3 dimensiones de una viga curva.

Los enlaces a los otros tres artículos en orden son:
– Voladizo circular (parte1) – Matrices de rigidez local
– Voladizo circular (parte2) – Matrices de rigidez global de toda la estructura
– Voladizo circular (parte3) – Vector de cargas
Sistema lineal de ecuaciones
Obtenidos la matriz de rigidez de toda la estructura y el vector de cargas, solo queda armar el sistema de ecuaciones:
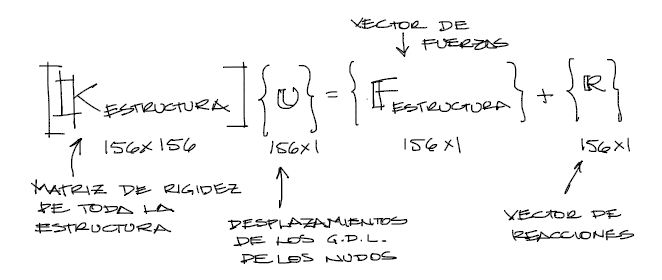
El sistema de ecuaciones se puede descargar del ENLACE. No es posible mostrar todo el sistema de ecuaciones en imagen por el tamaño relativamente grande de todo el sistema.
Las reacciones se adicionan al sistema como incógnitas. Existirán reacciones justo en los grados de libertad donde los desplazamientos son restringidos (U=0 entonces R=incógnita) (U=desconocido entonces R=0)
Reducción de grados de libertad restringidos
Como es bien sabido dentro del cálculo matricial, la matriz de rigidez de 156×156 es una matriz singular (con infinitas soluciones). La única manera de encontrar una solución específica relacionada a las condiciones de contorno es “apoyar” la estructura que de otra manera se encuentra flotando en el espacio sin un apoyo.
Los grados de libertad restringidos corresponden a todos los grados de libertad con apoyos empotrados.
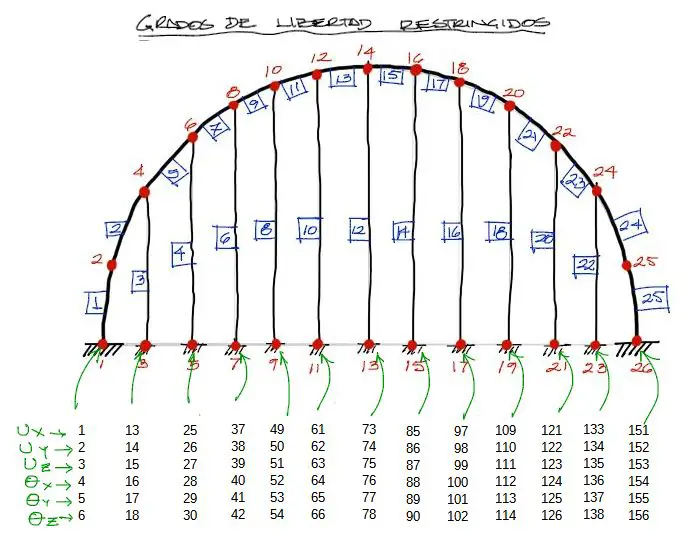
Los grados de libertad restringidos por nudo son 6: tres desplazamientos ux uy uz y tres giros θx θy θz, y se muestran en la figura arriba.
Estos grados de libertad restringidos corresponden a las filas y columnas que deben anularse en el sistema de ecuaciones de 156×156. Una vez anuladas estas filas y columnas nos quedamos con un sistema de ecuaciones de 78×78. El sistema de ecuaciones se ve más o menos como en la imagen siguiente, obtenida del arreglo en excel, y alejado al zoom más pequeño.

El sistema de ecuaciones muestra un arreglo de argumentos en banda, que puede resolverse por varios métodos numéricos. Cuando las matrices son grandes, es más conveniente aplicar estos métodos dependiendo siempre del tamaño del sistema. Un sistema de 78×78 es aun pequeño, y puede resolverse por Gauss-Jordan.
Conceptualmente, el sistema de ecuaciones reducido se ve más o menos como sigue:
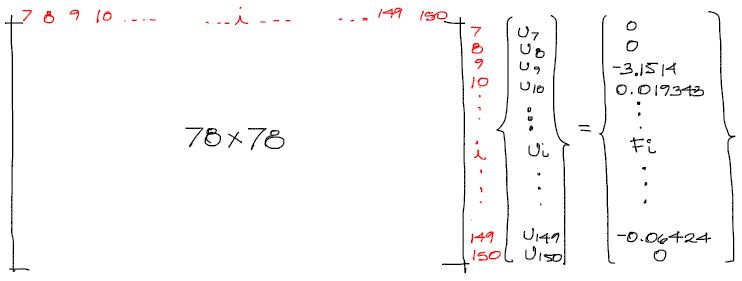
Notemos que el sistema de ecuaciones comienza en el grado de libertad 7, y se han suprimido todos los grados de libertad restringidos en el pórtico. Otro aspecto a notar es que las reacciones no entran en el sistema pues, como se mencionó antes, justo los grados de libertad anulados corresponden a las reacciones incógnita.
Solución al sistema de ecuaciones.
Luego de resuelto el sistema de ecuaciones por los métodos convencionales de resolución de sistemas lineales, obtenemos la solución de los desplazamientos de los nudos:

Obviamente los desplazamientos obtenidos arrancan desde el grado de libertad 7, pues son obtenidos a partir del sistema de ecuaciones reducido.
El paso siguiente consiste en completar los desplazamientos de los grados de libertad restringidos para contar con el vector completo de desplazamientos de dimensión 156×1 y graficar los resultados.

La gráfica mostrada fue realizada, al igual que el resto de los cálculos, en GNU-OCTAVE. Un software de cálculo matricial que menciono mucho en mi canal de youtube y en esta página web.
Reacciones
A partir de los 156 desplazamientos de los 156 grados de libertad, podemos encontrar las reacciones del sistema de ecuaciones.
Rescatamos la matriz de rigidez de 156×156 de toda la estructura y armamos el sistema de ecuaciones original antes de reducirlo. Esta vez sin embargo ya con los desplazamientos como datos.
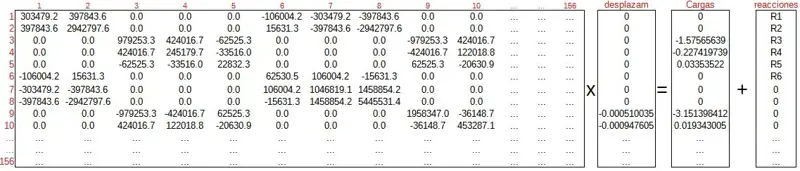
El motivo por el que aparecen las reacciones nuevamente es porque al momento de agregar los grados de libertad restringidos, 1 2 3 4 5 6 13 14… 155 156, se adicionan también todas las incógnitas de reacción eliminadas en la reducción del sistema.
Multiplicando [K_estructura]·{u} y despejando {R} llevando {F} al lado izquierdo de la igualdad, nos queda:
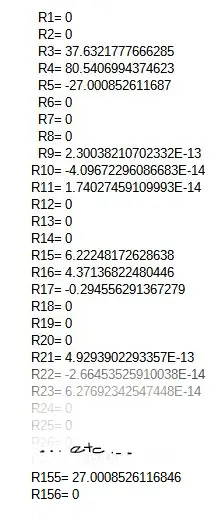
Estas reacciones pueden interpretarse de la siguiente manera. Por ejemplo para el nudo 1, con grados de libertad 1 2 3 4 5 6, estos grados de libertad son correlativamente Fx Fy Fz Mx My Mz en el apoyo del nudo 1. Para las reacciones diferentes de cero se tiene:
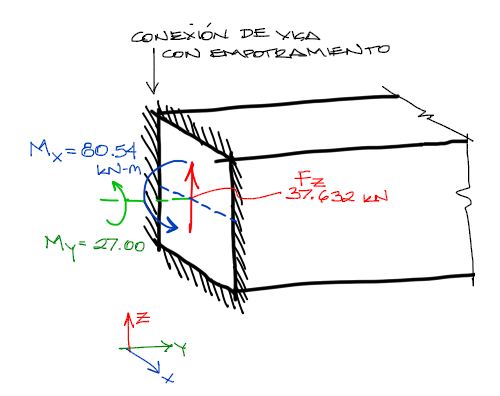
en el entendido de que por ejemplo el momento My corresponde a la reacción de momento de fuerza que gira al rededor del eje Y en el apoyo.
Para descargar
Todas las matrices y vectores mencionados en esta publicación pueden descargarse en ARCHIVOS.zip
Pasos siguientes:
Se debe a continuación obtener los momentos flectores, cortantes, fuerza axial y torsión en cada una de las barras y graficar los resultados. Esto se hará en siguientes publicaciones.
autor: Marcelo Pardo
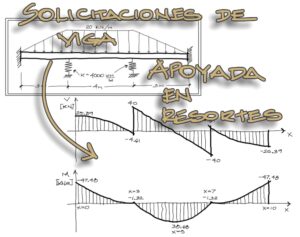

Muchas gracias por el aporte inge marcelo, de verdad es muy beneficioso para el aprendizaje. En un futuro llegará a mostrar la obtención y graficación de solicitaciones?
Sebastian, tengo un curso donde enseño justo como programar y plotear estos resultados de manera automática.
https://www.youtube.com/watch?v=kkVzLdV8lcM