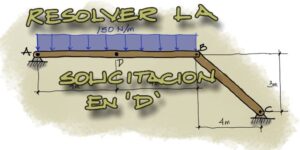
Enunciado
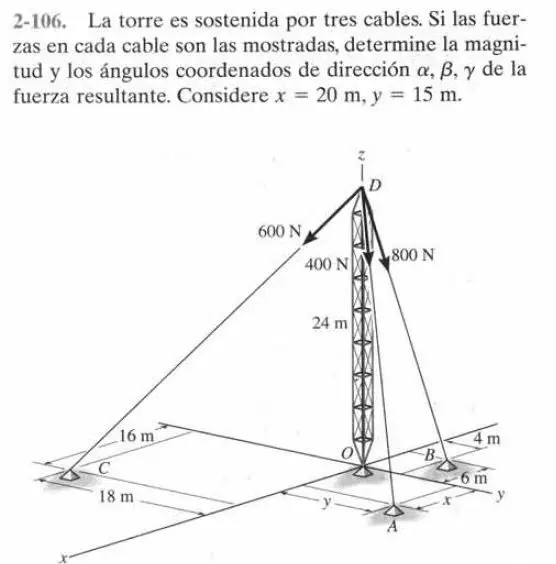
Solución analítica
El proceso de resolución de este tipo de ejercicios pasa por el siguiente número de pasos
- Encontrar vectores posición de cada punto de interés
- Calcular los vectores distancia, restando vectores posición, desde la punta del vector distancia hasta la cola del vector distancia
- Normalizar estos últimos vectores para que tengan una norma o módulo unitario. Esto se consigue dividiendo el vector entre su módulo

De esta manera se consiguen vectores “puntero” que apuntan en la misma dirección que los vectores fuerza cuyas componentes queremos conseguir.
Por tanto para conseguir las componentes de los vectores fuerza solo queda multiplicar los vectores unitarios por sus respectivos módulos de fuerza:
}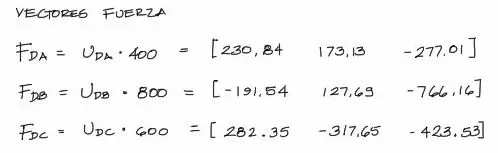
El enunciado pide encontrar el vector fuerza Resultante de las tres fuerzas, por tanto solo queda sumar las componentes de cada fuerza:

El último paso consiste en conseguir los ángulos directores del vector resultante. Para esto se encuentra el vector unitario del vector resultante dividiendo sus componentes entre su módulo, y luego sacando arccos de estas componentes del vector unitario.
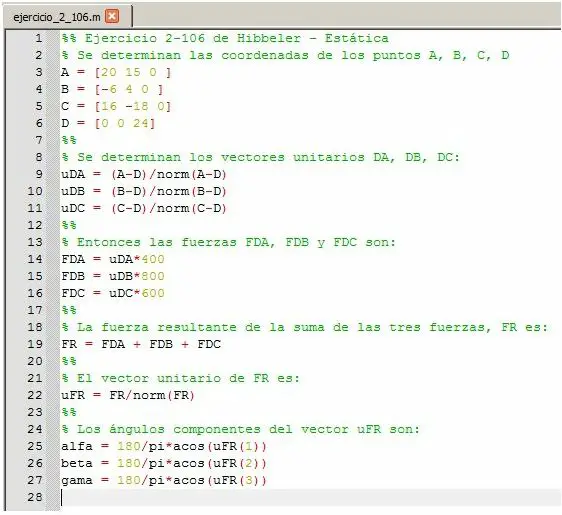
Solución con Matlab – Octave
Si se quiere aplicar la solución mediante operaciones con Matlab (Octave) entonces se puede seguir el siguiente procedimiento:
solo necesitas conocer los siguientes comandos:
- Asignar un vector a una variable: A = [x y z]
- Módulo de un vector: mod_A = norm(A)
- Para llamar la componente (digamos 1) de un vector: Componente=A(1)
← ← ← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL← ← ←
← ← ← VOLVER A TABLA DE CONTENIDO DE OCTAVE – MATLAB← ← ←
autor: Marcelo Pardo