Introducción
Las cerchas en 3 dimensiones trabajan a partir de matrices de rigidez deducidas en la publicación Teoría: Matriz de rigidez para elementos de cercha con deformación axial en 3 dimensiones.
En particular las cerchas solo reciben cargas en los nudos, y las solicitaciones obtenidas a partir de sus deformaciones son netamente axiales.
Planteamiento del problema
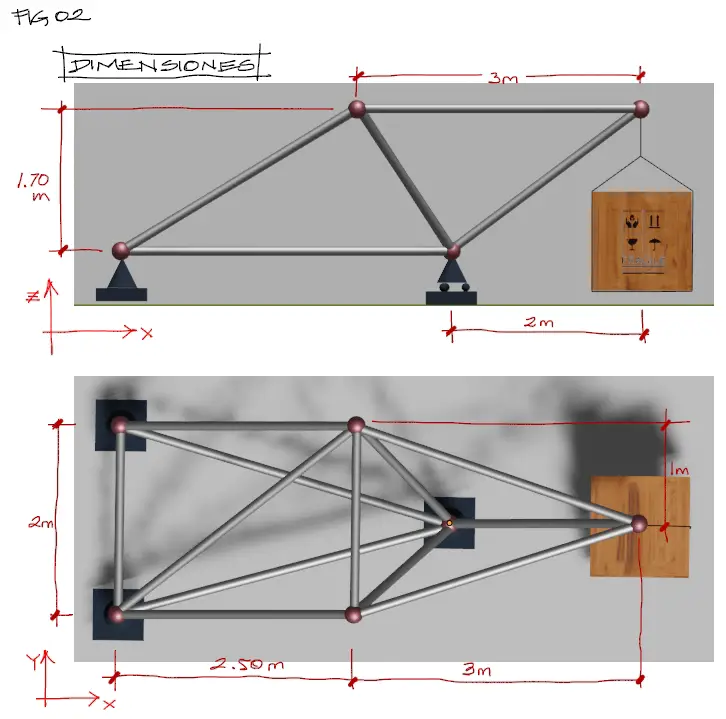
Se resolverá la cercha en 3 dimensiones mostrada en la figura:

Las secciones de los elementos es de tubo circular de 3″ y 1/4″ de espesor. El módulo elástico de la barra será de 200 [GPa]. La carga de la caja que soporta la estructura pesa 100 KN. Despreciar el peso propio de la estructura.
Las dimensiones de la cercha se muestran a continuación:
Solución
Los pasos de resolución de este tipo de estructuras es bastante mecánico. Se seguirán los siguientes pasos:
- Numerar nudos y barras
- Obtener longitud y ángulos directores de cada barra
- Calcular las matrices de rigidez de cada elemento
- Calcular la matriz de rigidez de toda la estructura
- Construir vector de cargas
- Armar el sistema de ecuaciones reducido y encontrar desplazamientos
- Encontrar reacciones de apoyos
- Calcular las solicitaciones de cada barra
Se irán tocando todos estos pasos a continuación
1) Numeración de nudos y barras
Identificaremos tanto nudos como barras de la manera mostrada en la figura siguiente:
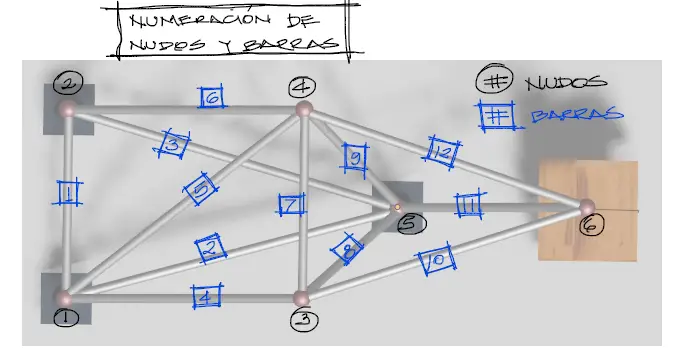
Se debe tomar en cuenta en la numeración de elementos, que lo más apropiado es barrer la numeración de izquierda a derecha y de abajo hacia arriba, procurando no volver hacia elementos que hayamos dejado atrás en el barrido. En estructuras grandes esto evita que nuestra matriz de rigidez tenga una banda muy ancha de elementos diferentes de cero.
2) Obtener Longitud y ángulos directores de cada barra
Lo primero que debemos tener antes de obtener las longitudes de cada barra, son las coordenadas de los nudos. Estas las deducimos por simple inspección del enunciado.
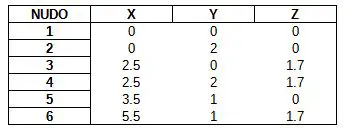
Para entender el procedimiento trabajaremos de ahora en adelante con una barra que nos permita acompañar todos los cálculos. Se supone que para las otras barras el cálculo será igual. La barra tipo sobre la cual haremos todos los cálculos será la barra #5
Para obtener la longitud de la barra, vamos a aplicar pitágoras en 3 dimensiones:
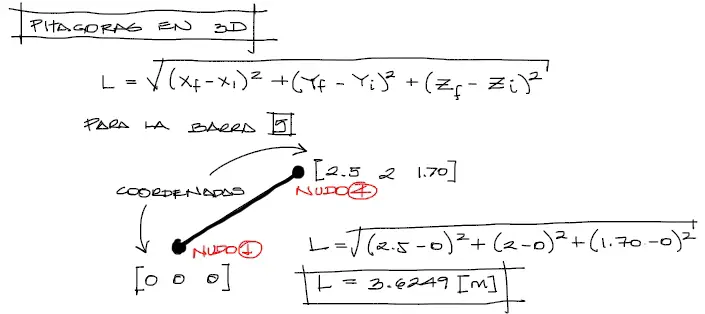
Con el dato de la longitud de la barra, se pueden obtener a continuación los ángulos directores que describen para la barra, la dirección exacta en la cual apunta esta. A partir de trigonometría:
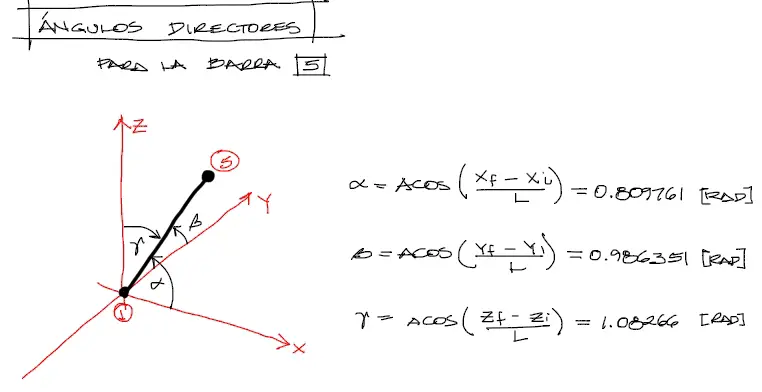
Se debe proceder de la misma manera para todos los otros elementos. Al final de este artículo está el archivo disponible para descarga de los cálculos para todas las barras.
Adicionalmente, la sección transversal de la barra 5 (que es igual para todas las otras) se calcula a partir de:
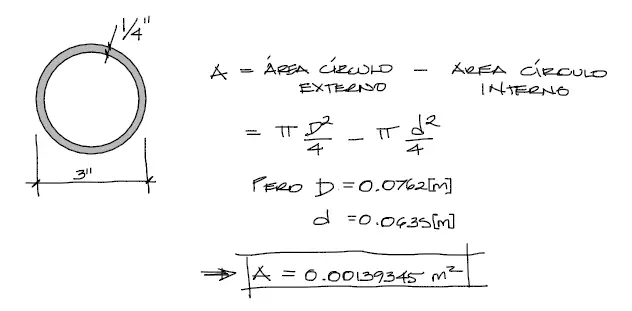
3) Matriz de rigidez del elemento.
La teoría de matrices de rigidez para un elemento de barra articulado en ambos extremos se puede encontrar en la publicación que hice de MATRIZ DE RIGIDEZ DE ELEMENTO DE CERCHA EN 3D. Te recomiendo darle un vistazo a esa publicación para entender el cálculo de estas matrices.
La matriz de rigidez del elemento 5 en coordenadas locales, que es el que estamos usando como ejemplo, será:
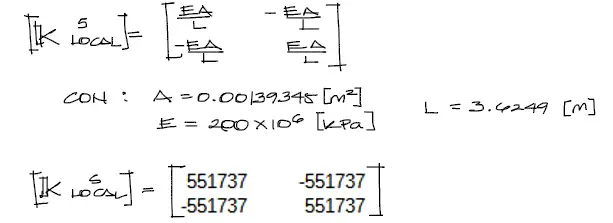
Debemos notar que se han calculado las secciones en las barras en m² y el módulo elástico en KPa. esto se debe a que debemos uniformar las unidades respecto a las cotas y a las cargas del enunciad, que están respectivamente en metros y en KN.
Ahora con los ángulos directores de la barra 5, podemos calcular la matriz de transformación [B]:

A partir de la matriz [K_local] del elemento 5 y su respectiva matriz de transformación [B] ya podemos calcular la matriz de rigidez de este elemento en coordenadas globales:
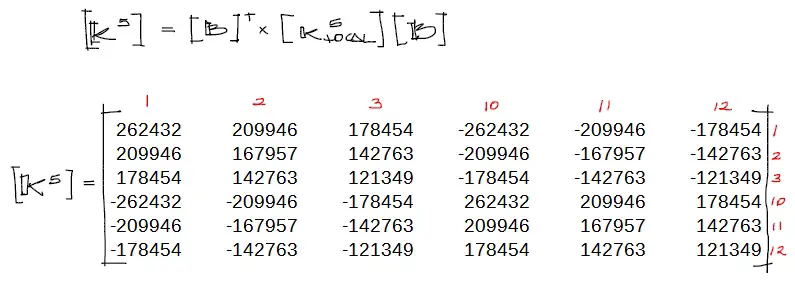
Los números rojos encima y al costado derecho de la matriz de rigidez calculada corresponden a los grados de libertad de arranque y llegada de cada barra. Estos grados de libertad se muestran en la siguiente imagen:
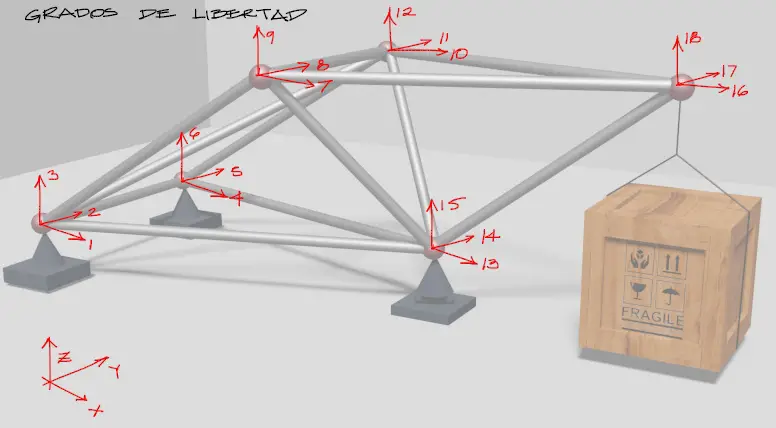
Como mencioné arriba, las matrices de ridigez de cada elemento se encuentran en el documento descargable al final del artículo.
4) Matriz de rigidez de toda la estructura
Se van transportando todos los elementos de las matrices de rigidez [K] en coordenadas globales de cada elemento hacia la matriz [K_estructura] que contiene las propiedades de deformación-fuerza de toda la estructura. Si dos elementos de diferentes matrices caen dentro de una misma casilla en [K_estructura] los dos elementos se suman.
La matriz resultante es bastante grande, por lo que en esta imagen se la grafica solo esquemáticamente:
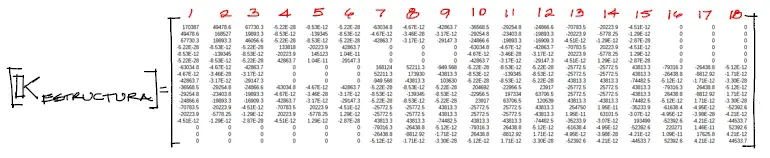
5) Vector de cargas
Como se menciona el enunciado, se puede despreciar el peso propio de la estructura. Además la única carga aplicada en la estructura corresponde a la de la caja mostrada en la imagen. La carga hacia abajo coincide con el grado de libertad 18 en la dirección negativa. Por tanto el vector de cargas será el de la imagen siguiente. Además se arma un vector de reacciones que se suma a las cargas, donde las incógnitas de reacción corresponden a los grados de libertad restringidos por los apoyos.
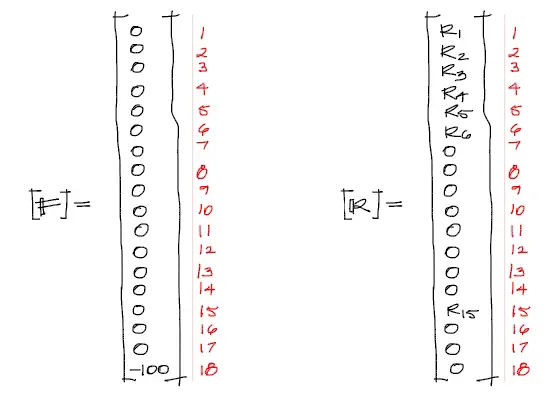
6) Armar el sistema de ecuaciones reducido y encontrar desplazamientos
El sistema de ecuaciones de toda la estructura se arma a partir de todos los datos encontrados hasta ahora. El sistema de ecuaciones completo se ve más o menos como sigue. Entendamos que no podemos anotar todos los elementos de la matriz de rigidez por tratarse de demasiados elementos.
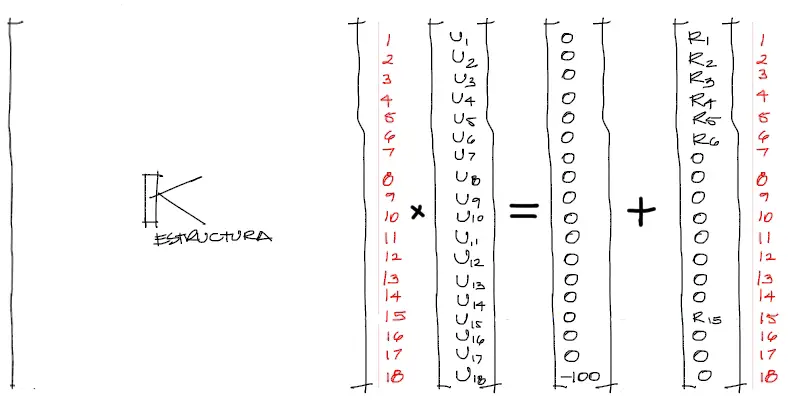
Se deben anular los grados de libertad restringidos por los apoyos. Se puede ver que los grados de libertad 1, 2, 3, 4, 5, 6 corresponden a los grados de libertad de los apoyos fijos de los nudos 1 y 2. A diferencia de estos nudos, el nudo 5 solo tiene restringido el grado de libertad 15, por tanto anulamos filas y columnas de todos los GDL mencionados.
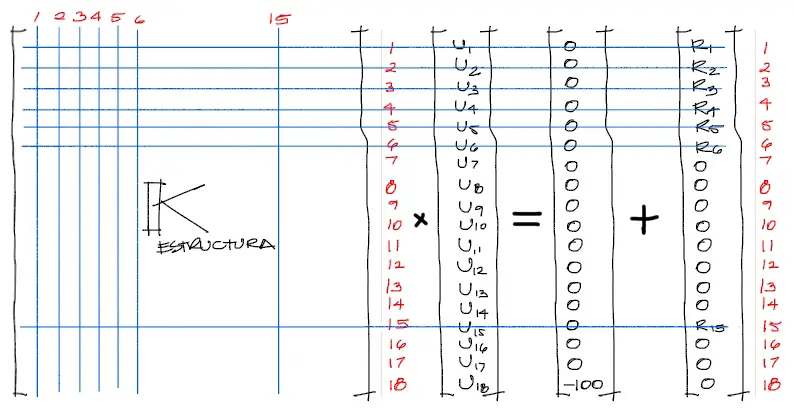
Luego reescribimos el sistema de ecuaciones:
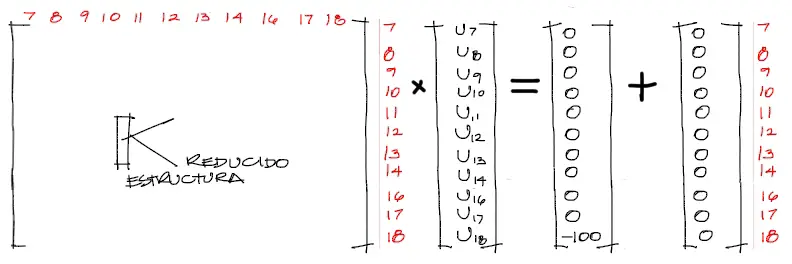
Resolviendo el sistema de ecuaciones obtenemos todos los desplazamientos de los grados de libertad restantes:

7) Encontrar reacciones en los apoyos
Este paso ya es sencillo a partir de los datos encontrados. Simplemente se deben reemplazar los desplazamientos encontrados dentro del sistema de ecuaciones de 18×18 y despejar el vector de reacciones. De esa forma se obtiene lo siguiente:
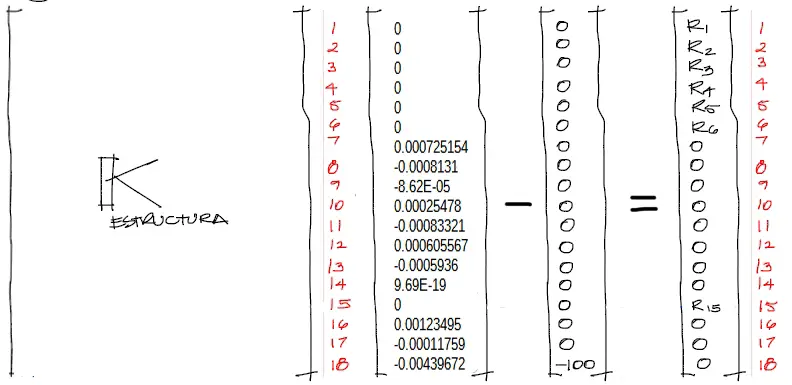
Operando tenemos:
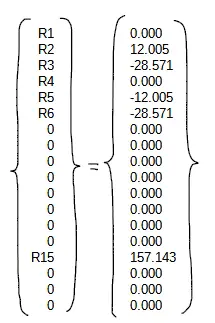
8) Calcular las solicitaciones de cada barra
El último paso consiste en el cálculo de solicitaciones de cada barra. En este caso por tratarse de elementos de cercha, solo tendrán solicitaciones axiales.
Trabajaremos como en todo el problema, con el elemento 10 ya que las solicitaciones para el elemento 5 son nulos.
Primeramente debemos transformar los desplazamientos globales correspondientes al elemento 10, en desplazamientos locales, multiplicando la matriz de transformación por los desplazamientos globales:
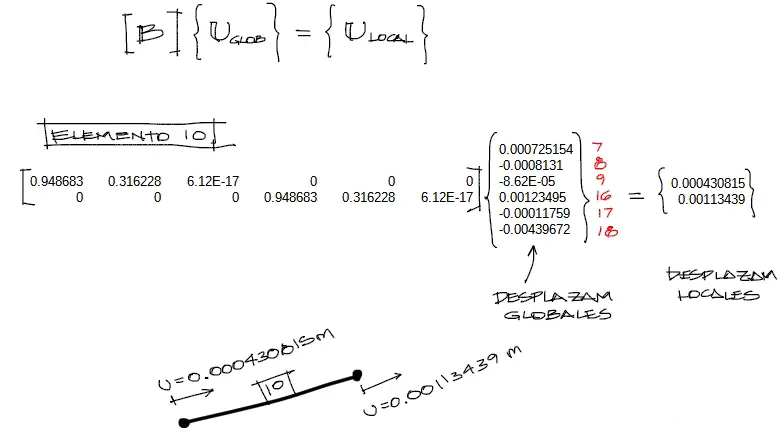
con estos desplazamientos, podemos conocer las solicitaciones en la barra multiplicando [K_local]*[uLocales]:
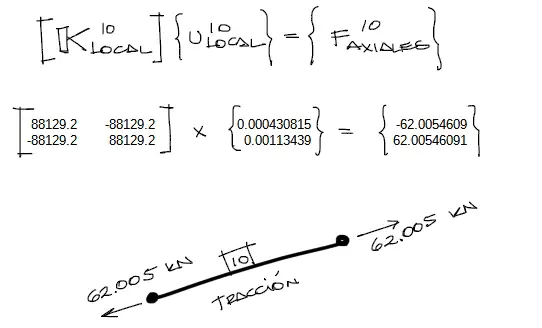
Solicitaciones de toda la estructura
repitiendo el paso 8) para todos los elementos de la estructura, obtenemos el siguiente resultado:
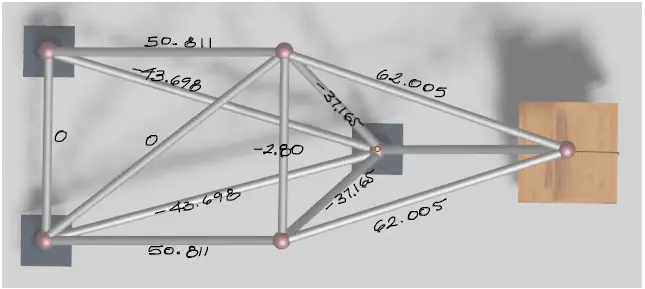
y con esto termina el ejercicio de resolución de cercha en 3d
Resultados para descargar
Los resultados para descargar en archivo de texto los puedes obtener en el PRESENTE ENLACE
autor: Marcelo Pardo