¿Dónde estamos parados?

Es difícil escribir todo un artículo sobre graficación de solicitaciones en pórticos o vigas sin ponernos en contexto. Y eso es justamente lo que intentaré hacer aquí.

Hasta este punto se supone que hemos resuelto todos los desplazamientos de los nudos de una estructura completa con tramos articulados de viga o de columna, mediante el método matricial. No vamos a explicar todo ese proceso pues es largo, sin embargo si has llegado hasta este punto, ya tienes la idea más o menos clara del proceso.

Sin embargo voy a dejarte unos enlaces de información que te puede ser útil, además de un curso que ya es bastante conocido sobre resolución de pórticos por el método matricial:

• – Curso de Programación de pórticos en Matlab y GNU Octave
• – Resolución de Pórtico con articulaciones – PARTE I
• – Resolución de Pórtico con articulaciones – PARTE II
• – Resolución de Pórtico con articulaciones – PARTE III

La resolución de un pórtico por el método matricial con elementos articulados es similar al de un pórtico sin articulaciones. En la etapa de encontrar los desplazamientos lo único distinto es el reemplazo de la matriz de rigidez de elemento de pórtico por un elemento de pórtico articulado. Dependiendo de si el pórtico está articulado a la izquierda, a la derecha o en ambos extremos, la matriz de rigidez de este elemento será distinta. Las tres matrices te las dejo a continuación:
– Matriz de rigidez de elementos articulados en pórticos

Una vez resueltos entonces los desplazamientos de nuestro pórtico articulado, debemos encontrar las solicitaciones de cada barra.

Las ecuaciones de Momento, cortante y deflexión

Existen varias maneras de obtener las solicitaciones en un tramo de pórtico cuando ya tenemos los desplazamientos de los nudos. Sin embargo considero que la manera más adecuada es a partir de la ecuación de la elástica integrada 4 veces:

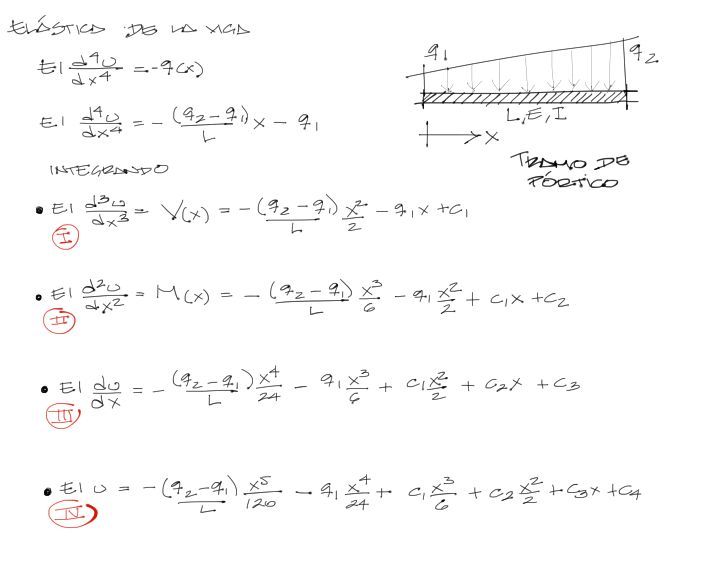
donde:

• u: desplazamiento vertical en cualquier punto del tramo
• EI: rigidez
• L: longitud de la viga
• x: coordenada local del tramo. x=0 a la izquierda y x=L a la derecha
• I: La primera integral corresponde al cortante del tramo
• II: La segunda integral corresponde al momento flector del tramo
• III: La tercera integral corresponde a la pendiente de la deflexión del tramo
• IV: La cuarta integral corresponde a la deflexión del tramo

Con estas ecuaciones se conoce el comportamiento completo de la viga en cuanto a solicitaciones. Las únicas incógnitas en estas ecuaciones son las constantes de integración que se generan al integral la elástica.

Dependiendo de si el tramo es articulado o no, se pueden encontrar estas constantes a partir del análisis de los siguientes apartados.

Solicitaciones de barra sin articulaciones

Cuando no existen articulaciones en los extremos del tramo, se puede seguir un procedimiento similar al explicado en el siguiente enlace: Cortantes y Momentos flectores a partir de desplazamientos y giros en extremos de una viga.

Si bien el artículo citado está configurado para encontrar las ecuaciones de momento y cortante para un tramo de viga, este proceso es fácilmente extrapolable a un tramo de pórtico simplemente cambiando los nombres de los desplazamientos, y cambiando las coordenadas x=x1 y x=x2 a x=0 y x=L respectivamente. Queda entonces un tramo de pórtico con los siguientes datos:

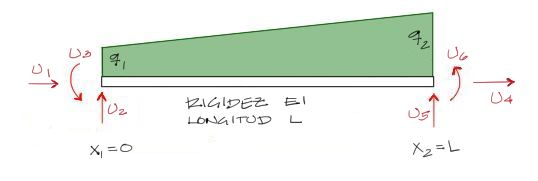
• q1: Inicio de la carga trapezoidal
• q2: Fin de la carga trapezoidal
• EI: rigidez del tramo (constante)
• L: Longitud del tramo
• u1, u2, … u6: desplazamientos de los nudos extremos

Para una viga sin articulaciones en los extremos, el sistema de ecuaciones que nos ayudará a encontrar estas constantes de integración C1, C2, C3, C4 es la siguiente:

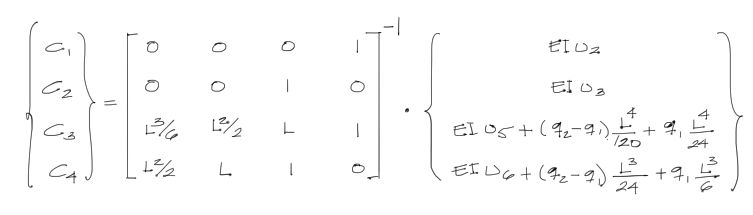
Este sistema de ecuaciones se obtiene a partir de las ecuaciones de la elástica y las condiciones de contorno explicadas en el artículo citado arriba, y cambiando x1 por 0, x2 por L, y renombrando los desplazamientos verticales y giros.

Solicitaciones de barra con Articulación derecha

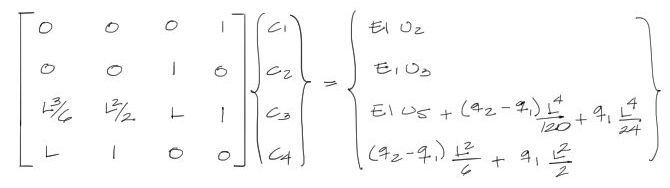
El procedimiento para encontrar las constantes de integración para esta situación es algo distinto al anterior en la definición de las condiciones de contorno. En este caso no se conoce el giro en la articulación derecha, pero se sabe que el momento flector es cero. Por tanto se procede como se muestra en el siguiente enlace:

En resumen, para encontrar las constantes de integración y reemplazarlas en las ecuaciones de la elástica de arriba, se debe resolver el siguiente sistema:

Solicitaciones de barra con Articulación izquierda

De igual manera, dejo a continuación todo el procedimiento de deducción de las fórmulas para encontrar las constantes:

En resumen, para encontrar las constantes de integración y reemplazarlas en las ecuaciones de la elástica de arriba, se debe resolver el siguiente sistema:

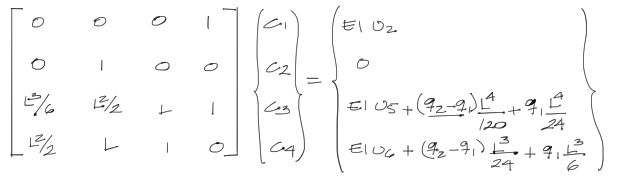
Solicitaciones de barra con Articulación en ambos extremos

De igual manera, dejo a continuación todo el procedimiento de deducción de las fórmulas para encontrar las constantes:

En este caso, para encontrar las constantes de integración y reemplazarlas en las ecuaciones de la elástica de arriba, se debe resolver el siguiente sistema:

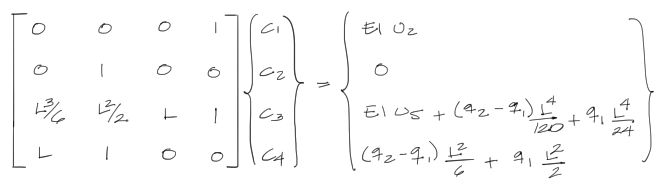
Último paso

Como se dijo antes, una vez encontradas las constantes C1 a C4, estas últimas se reemplazan en todas las ecuaciones de la elástica para así obtener cortante, momento flector, pendiende de deflexión y deflexión de la viga para cualquier punto “x” entre 0 y L para dicho tramo. El mismo procedimiento debe aplicarse para todos los tramos del pórtico en análisis.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS ←←←