Introducción

Uno de los métodos de resolución de diagramas de momento y cortante de vigas isostáticas parte de la resolución del equilibrio del corte de la viga, como el mostrado en la siguiente figura. Se realiza un corte a una distancia “x” desde el extremo izquierdo de la viga y se equilibra el corte.

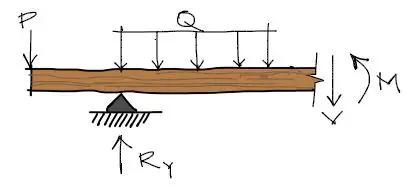
Luego se equilibra el corte tanto para ΣFx=0 , ΣFy=0 , ΣM=0.

Sin embargo, el método sistemático para encontrar diagramas de momento flector y cortante en programas computacionales está basado en la teoría de la elástica de la viga y en métodos matriciales de análisis que pueden automatizar el proceso de cálculo.

La ecuación de la elástica

La ecuación de la elástica de la viga consiste en una ecuación diferencial de cuarto orden que resuelta nos entrega las deflexiones de la viga. En su forma diferencial la ecuación se ve de la siguiente manera:

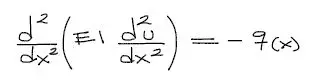
Donde:
I = inercia de la sección transversal de la viga (puede variar en función de x)
E = Módulo elástico de la viga (puede variar en función a x)
x = coordenada horizontal medida desde el extremo izquierdo de la viga
u = Deflexión o desplazamiento vertical del eje de la viga en un punto “x”
q(x) = carga distribuida en función de “x”. La ecuación está concebida para una ecuación de carga gravitacional.

Esta ecuación es de fácil resolución siempre que la viga sea de pocos tramos y no tenga discontinuidades de apoyo o de carga puntual. Sin embargo a pesar de su utilidad restringida a vigas sencillas, hiperestáticas o isostáticas, su compresión conceptual es de gran ayuda para entender problemas más complejos.

Resolución de la ecuación de la elástica

Para resolver la ecuación diferencial mencionada, naturalmente debemos integrarla. Y debido a que la variable diferencial se encuentra solo al lado izquierdo de la ecuación, la integración es inmediata. Integrando 1 vez entonces, tenemos:

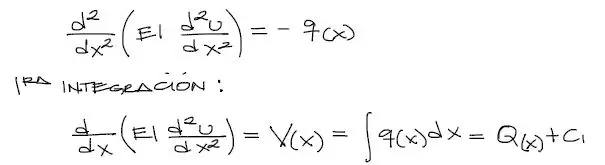
La primera integral de la ecuación de cuarto orden resulta en una ecuación de tercer orden que representa el cortante de la viga denotado por V(x). A la derecha de la ecuación se genera una constante de integración C1 y una función de Q(x) integrada desde q(x).

Integrando por segunda vez esta última ecuación se tiene:

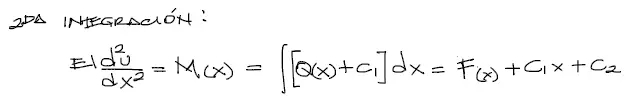
Esta segunda ecuación integrada representa el momento flector de la viga M(x). Al lado derecho de la ecuación debemos integrar la función. La integrada de Q(x) llamaremos F(x) y a la vez se genera una segunda constante de integración C2.

Integrando una tercera vez:

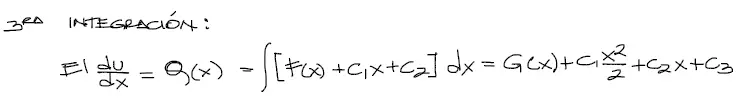
Esta tercera ecuación integrada representa la pendiente de la viga θ en cualquier punto de la viga. Al lado derecho integrando F(x) obtenemos otra función G(x) y una tercera constante que se genera C3.

Finalmente integrando una última vez obtenemos la ecuación de la elástica de la viga “u”.

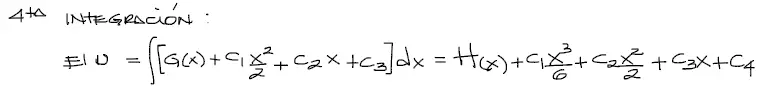
Al lado derecho se integra G(x) obteniendo H(x) y además una cuarta constante de integración C4.

Qué son las constantes de integración

Si nos fijamos detenidamente, si conocemos la ecuación de la carga distribuida, podriamos conocer las ecuaciones de momento M(x), cortante V(x), o pendiente y deflexión de la viga al momento de integrar la ecuación 4 veces. Sin embargo se generan nuevas incógnitas por determinar C1, C2, C3, C4.

Estas constantes de integración representan incógnitas que se definen en función a las condiciones de borde de la ecuacíón diferencial. Las condiciones de borde de una ecuación diferencial tienen un significado específico en el caso de vigas: Se refieren a los apoyos de la viga.

Para entender las condiciones de borde o de contorno a aplicar a estas ecuaciones, debemos entender lo siguiente.

Tipos de apoyos y condiciones de contorno

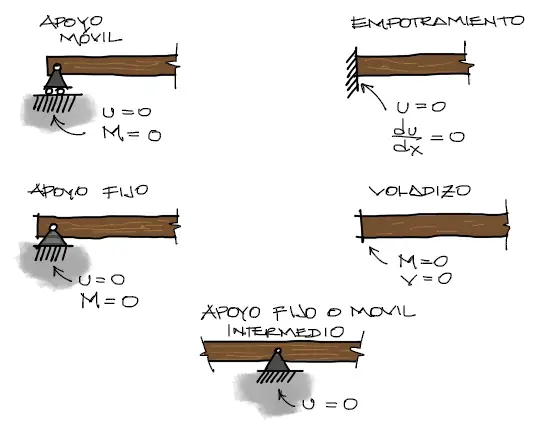
Según la configuración del apoyo, se pueden establecer ciertos valores conocidos de momento flector, cortante, deflexión o pendiente en estos puntos.

Por ejemplo si en la viga existe un apoyo empotrado, sabemos que en este punto de empotramiento, la viga no se desplaza hacia abajo (deflexión U = 0) y tampoco gira (pendiente θ=du/dx=0). De la misma manera se pueden deducir diferentes condiciones para diferentes tipos de apoyo:

Resolución de Constantes de integración

Existen 4 constantes de integración por averiguar en nuestra ecuación elástica, y por tanto necesitamos 4 condiciones de contorno para encontrarlas. Estas ecuaciones de contorno las obtendremos de la configuración de apoyos de la viga y deberemos reemplazarlas dentro de las ecuaciones integradas. Obviamente, si en la configuración de apoyo tenemos M=0, deberemos reemplazar M=0 en la 2da ecuación integrada. Si tenemos una condición de u=0, deberemos reemplazar esta condición en la última ecuación (4ta) integrada.

Se pueden reemplazar dos condiciones de contorno dentro de la misma ecuación, una a la vez. Por ejemplo:

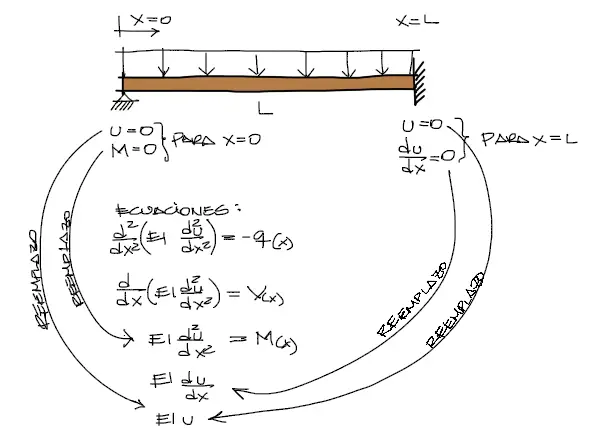
De esta manera se obtienen 4 ecuaciones con 4 incógnitas. Se resuelve el sistema de 4×4 y el ejercicio termina con las ecuaciones resueltas y listas para graficar.

Cuando hay más de un tramo

Existen casos donde se generan discontinuidades en la viga, que “cortan” las ecuaciones de diagramas de momento, cortante, deflexión y pendiente.

Estas discontinuidades, pueden ser apoyos intermedios en la viga, pero también pueden ser cargas puntuales (de fuerza o de momento de fuerza) o inicio y final de una carga distribuida. En estos casos, la viga debe dividirse en función a las discontinuidades que se presenten y debe asignarse una ecuación diferencial por entre 2 discontinuidades.

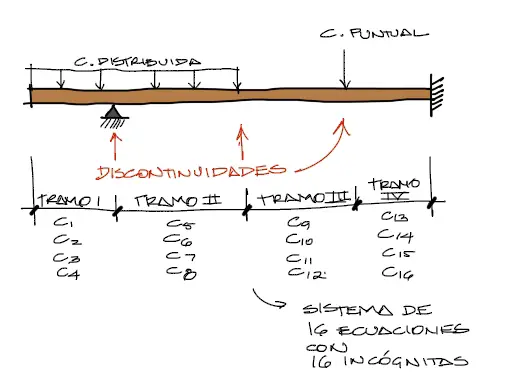
Mientras más discontinuidades existan, más constantes de integración se generarán y más grande será el sistema de ecuaciones a resolver a tal punto de volverse un método poco práctico para una viga de muchos tramos o de muchas discontinuidades.

A la vez, la definición de condiciones de contorno se hace compleja. Sin embargo no es imposible resolver vigas por este método para vigas de varios tramos.

Ejemplo

Varios ejemplos de este método pueden analizarse en los SIGUIENTES ENLACES:

Ejemplo 1 de viga Hiperestática Por método de la Elástica
Resolución de viga hiperestática con carga puntual por el método de la elástica.
Ejemplo de Viga de 2 tramos por método de la Elástica

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL←←←

←←← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES ←←←