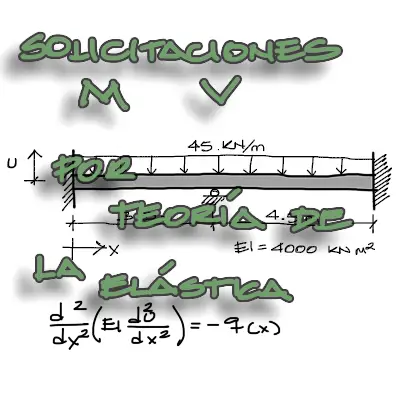
Enunciado

Se pide encontrar el diagrama de delexiones y el diagrama de momentos flectores para la viga sometida a cargas mostrada en la siguiente imagen. Utilizar el método de integración de la ecuación de la elástica para su resolución

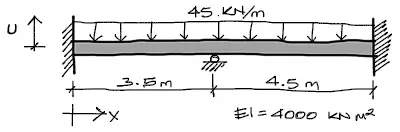
Resolución

Paso 1 – integración

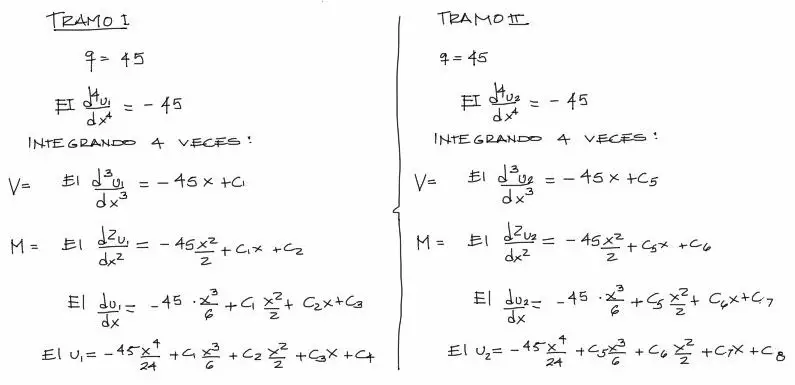
Debido a que en la viga se tienen dos tramos, se necesitan dos juegos de ecuaciones para integrar. La carga es distribuida constante por tanto la carga q(x) será también constante, y vale 45.

Reemplazando este dato en la ecuación de la elástica para cada tramo e integrando, se tiene:

Paso 2 – Condiciones de contorno

Para cada tramo se tienen ciertas condiciones de contorno dadas por los apoyos de la viga. En empotramiento los desplazamientos “u” y su pendiente du/dx, son cero. En cambio en apoyos móviles solo “u” es igual a cero. Con esto en mente, se tiene:

En la integración de las ecuaciones de la elástica se vió que existen 8 constantes de integración por tanto se necesitan 8 condiciones de contorno. Se encontraron sin embargo solamente 6.

Las otras dos condiciones salen de la interacción entre ambos tramos. Donde se unen el tramo 1 y tramo 2, el momento flector es coincidente. Además las pendientes de ambos tramos en la unión de tramos es igual. Se tiene entonces:

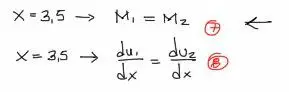
Paso 3 – Reemplazo de valores

Con las condiciones de contorno y las ecuaciones de la elástica, se tienen 8 ecuaciones con 8 incógitnas (las constantes de integración) para resolverlas en un sistema. Armando el sistema de ecuaciones se tiene entonces:

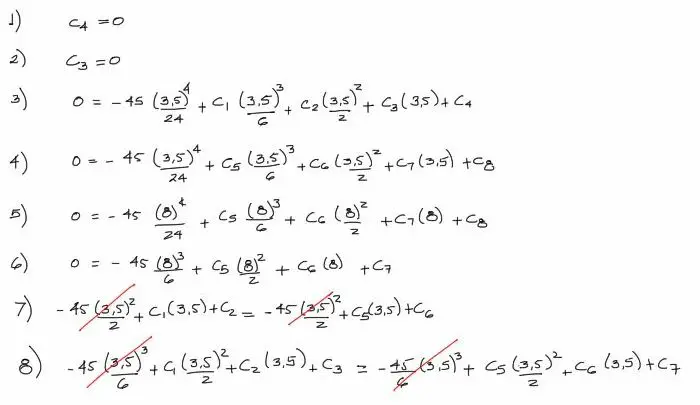
Si se escribe este mismo sistema en un arreglo matricial, por comodidad, se tiene:

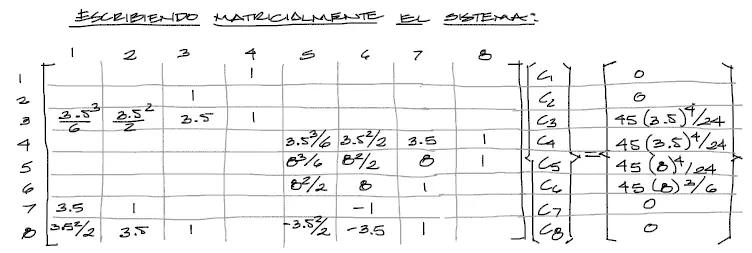
Si lo tuyo es el uso de Matlab como herramienta para la resolución de sistemas de ecuaciones, el código .m que nos ayuda a resolver el sistema puede escribirse como sigue:

Y resolviendo el sistema se obtienen las 8 constantes de integración.

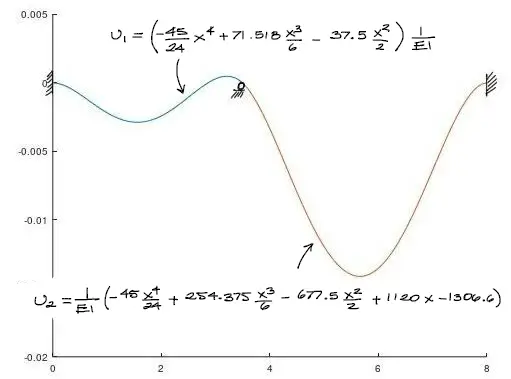
Paso 4 – Graficación

Obtenidas las ecuaciones de contorno para el problema, se reemplazan las condiciones en las ecuaciones arriba justo después del enunciado. De esta manera se tienen las ecuaciones resueltas tanto de momento flector, Cortante, pendiente de deflexión y deflexión.

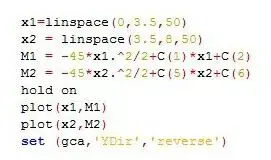
Nuevamente, si eres fan de Matlab, el código que te ayudará a graficar las ecuaciones, es:

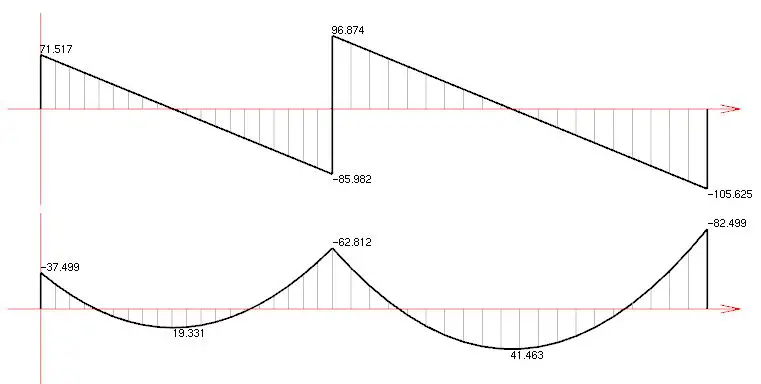
Luego, el resultado es el siguiente:

Lo mismo se puede hacer para los momentos flectores:

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL←←←