Enunciado
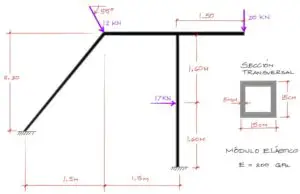
El ejercicio consiste en resolver los desplazamientos, reacciones y solicitaciones del pórtico mostrado a continuación
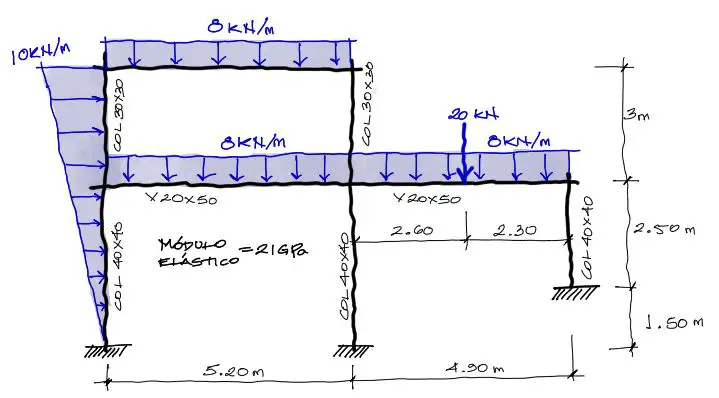
Además enumeramos los grados de libertad de los nudos de la forma mostrada a continuación. Esta numeración nos servirá en lo posterior.
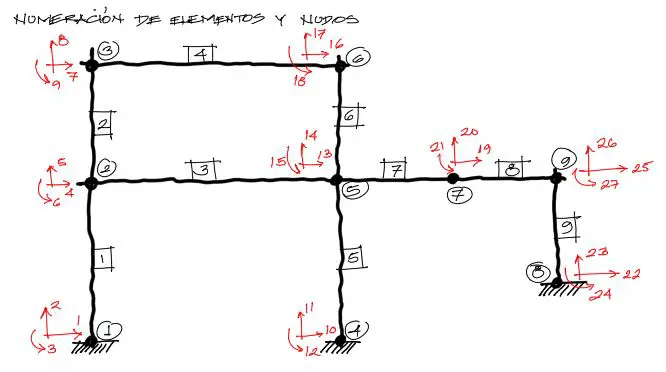
Pasos previos
Hasta aquí se avanzó un largo camino comprendido por dos publicaciones anteriores:
– Ensamblaje de la matriz de rigidez
– Vectores de carga
Si no viste los artículos mencionados, debes dirigirte a ellos antes de continuar.
Resolución del sistema de ecuaciones
El sistema de ecuaciones [K]{u} = {F}+{P} es un sistema de 27 ecuaciones lineales con 27 grados de libertad, por tanto con 27 incógnitas. Sin embargo este sistema tal como está, tiene infinitas soluciones, debido a que la matriz K es singular.
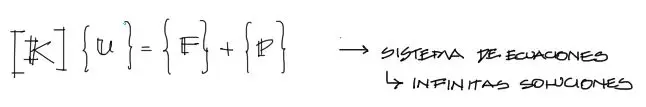
La explicación física de una matriz singular indica que puede adaptarse a diferentes condiciones de contorno o que los apoyos no están definidos.
Para definir los apoyos en el sistema de ecuaciones se debe imponer la condición de desplazamiento cero a los grados de libertad restringidos. Esto implica hacer cero a los desplazamientos de los nudos empotrados. Así, se logra un sistema de ecuaciones reducido que ya tiene una sola solución particular.

De este sistema de ecuaciones se puede despejár el vector de desplazamientos multiplicando por delante a ambos lados la matriz de rigidez reducida K-red inversa. El despeje queda como se muestra en la anterior imagen.
Si se fija uno en los grados de libertad de los empotramientos, estos corresponden a los GDL 1,2,3 para el primer nudo, 10, 11, 12 para el nudo 4 y 22, 23, 24 para el nudo 8. Los desplazamientos de estos grados de libertad igualados a cero en el sistema de ecuaciones anulan automáticamente las filas 1, 2, 3, 10, 11, 12, 22, 23, 24.
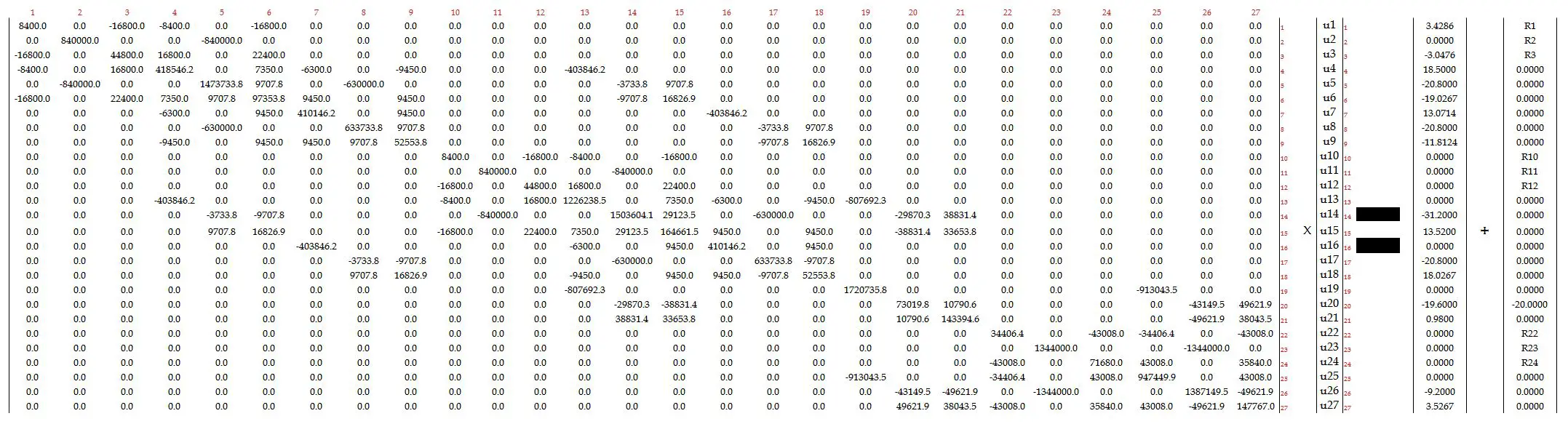
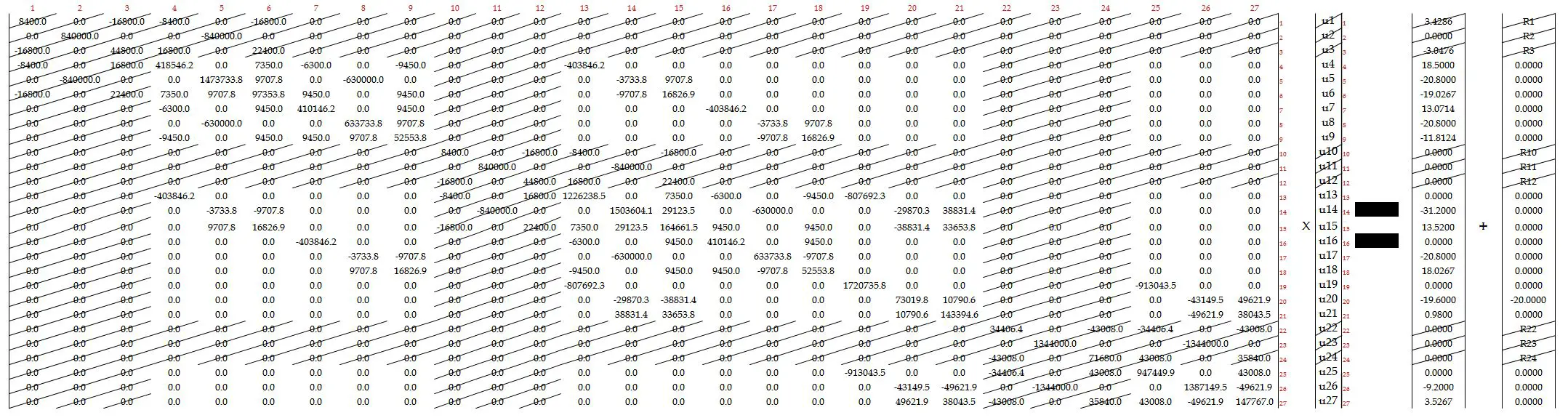
El sistema de ecuaciones sin reducir queda de la siguiente manera (puedes abrir la imagen en tamaño real haciendo click encima de la imagen):
El sistema de ecuaciones anulando los grados de libertad mencionados quedará así (agranda la imagen haciendo click encima de la imagen):
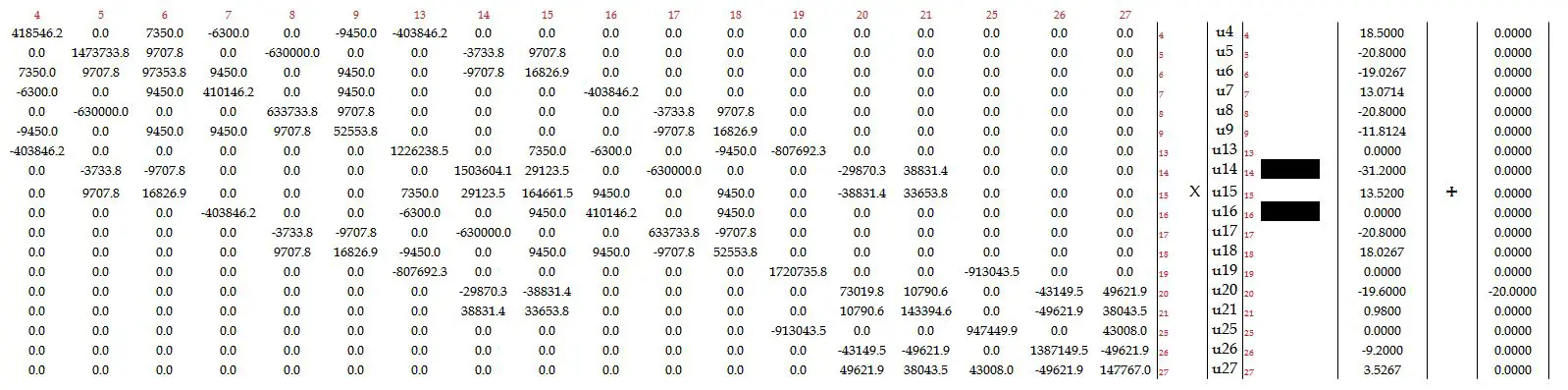
Y finalmente reduciendo las filas y columnas tachadas, queda:
Este sistema de ecuaciones ya puede resolverse fácilmente por cualquier método de eliminación gaussiana. Queda entonces el siguiente resultado:

En general el método de rigidez y de elementos finitos concentra sus más grandes esuferzos en la resolución de los desplazamientos del sistema que se analice. Luego, la resolución de las solicitaciones y reacciones a partir de estos desplazamientos se pueden obtener mediante el método que menciono en el artículo Momentos y cortantes a partir de desplazamientos en los nudos.
autor: Marcelo Pardo

Saludos Ingeniero, una inquietud, en el caso que en un elemento exista una carga axial uniformemente distribuida, como se procedería con las solicitaciones axiales?. También se aplicaría la formula de P=A*E*(u4-u1)/L, pero donde ya no consigo avance es al momento de aplicar la carga distribuida axial, para conseguir una función para graficar el diagrama de axiales.
Sebastian, para aplicar cargas axiales, la carga “f” axial uniforme se distribuye entre ambos nudos como “fL/2” en cada nudo. Efectivamente para encontrar la solicitación de cada barra se aplica la fórmula que tu citaste, una vez conocidos los desplazamientos u4 y u1
Muchas gracias ingeniero, una vez consigo la solicitación con la fórmula, que otro paso habría que seguir?, para que el diagrama no sea constante, ya que al existir una distribuida axial, el diagrama tendría que variar a lo largo de la barra
En ese caso se debe aplicar una carga distribuida “f” que se concentra en cada nudo como fL/2 en cada nudo. Este fL/2 se aplica en los vectores de carga de manera similar. Luego efectivamente tendrémos una transición de solicitaciones axiales no constante entre ambos nudos en la resolución del ejercicio.
Saludos ing. Marcelo, Entonces ya encontrados los desplazamientos, para encontrar los diagramas de momento, cortante y axial, se haría mediante la fórmula de la elasticidad?. La inquietud es hay que transformar los desplazamientos a coordenadas locales o simplemente con esos desplazamientos y las respectivas formulas??
Gracias por educarnos con sus conocimientos
Ronal, se necesitan transformar los desplazamientos a coordenadas locales.
Ronal Sánchez, Debes multiplicar la matriz de rigidez local de la barra que deseas obtener sus reacciones por el desplazamiento de los nodos que conectan la misma barra. Por ejemplo:
F1(Barra D)= K11D*Desp(1)+K12D*Desp(2)
F2(Barra D)= K21D*Desp(1)+K22D*Desp(2)
En donde K11,K12,K21 y K22 son las matrices de rigidez de esa barra en este caso D y Desp(1) y (2) son los desplazamientos inicial y final locales que corresponden a los desplazamientos de los nodos generales que encontrastre con el vector final de desplazamientos que obtuvo el Maestro Marcelo. Saludos!! 😀 y que la fuerza axial te acompañe.
Excelente aporte estimado Marcelo,saludos desde Ecuador.
Muchas gracias Mario! Un gran saludo
Ingeniero muchas gracias y mis felicitaciones, por el contenido del método, muy interesante y de gran ayuda, en el caso programar este método en un lenguaje básico de programación, cual seria de su sugerencia?? y que guias poder usar para el mismo programa??. De antemano muchas gracias
Raúl buen día. Te sugiero utilizar MatLab u Octave que vienen siendo lo mismo, solo que octave es gratuito.
Tengo un curso sobre resolución de vigas en 2D en el que explico todo el procedimiento de programación y el resultado son gráficas de momento y cortante. Te invito a que lo veas:
https://youtu.be/Eih5VA8Fj2s
si quieres más información me escribes al whatsapp por favor
+591 698 97074
Excelente aporte Marcelo !!,todo muy claro,ordenado y conciso.
Como sugerencia de tema me gustaría que hablaras de como aplicar corte basal en estructuras sin diafragma rígido.(algún ejemplo sencillo).
Saludos!.
Muchas gracias por comentar! claro que si. Comenzaré a escribir sobre análisis dinámico ni bien termine lo más básico de las ramas de mi página. Muchas gracias por el apoyo!