
Nota del autor
Esta publicación tiene ya algunos años. Consiste en la deducción de fórmulas que calculan la capacidad de resistencia a flexión de una viga que solo cuenta con acero a tracción.
La perspectiva de esta publicación es algo simplista ya que asume que la falla será por fluencia del acero siempre. Esto último no es del todo cierto ya que si el acero a tracción es muy grande respecto a la sección comprimida del concreto, es el concreto el que fallará antes que el acero, descendiendo el eje neutro hasta una distancia cercana a “d” y desarrollando resistencias más altas que las correspondientes al momento nominal Mn desarrollado por Asmax (como se ve al final de este artículo).
Este análisis no es tomado en cuenta en esta publicación (por simplicidad) y se limita a calcular la resistencia a flexión Mn para un acero máximo correspondiente a Acero máximo como fracción del acero balanceado.
Para tomar en cuenta el caso de falla frágil de concreto cuando el acero As es mayor As_max, hice una publicación extensa y más completa en el enlace:
TEORÍA DE REVISÓN DE RESISTENCIA DE VIGAS DE HORMIGÓN ARMADO
Hecha la aclaración, continua con el resto del artículo.
Propósito
Muchas veces, en vez de diseñar una viga y averiguar sus dimensiones, lo que se quiere es conocer la resistencia de una viga ya construida o ya calculada y mostrada en planos.
Este tipo de análisis está antes que el análisis de diseño de vigas pues es más sencillo de explicar y de desarrollar.
Nos ponemos en la situación entonces de que conocemos las cargas que llegan a la viga y por tanto podemos conocer los momentos solicitantes Mu que llegan a ella. Entonces necesitamos saber si la viga que ha sido concebida para sostener esa carga realmente puede resistir un momento de diseño ØMn mayor o igual a Mu. Para entender mejor estos conceptos de Mu y øMn te invito a leer mi anterior artículo Qué momento máximo resiste una viga de Hormigón Armado.
Datos necesarios para conocer el Momento resistente de diseño øMn
Para conocer este momento se necesitan los siguientes datos de la viga:
- b = ancho de la viga
- d = altura efectiva de la viga (distancia de la fibra más comprimida de hormigón al eje de los aceros a tracción
- fy = resistencia a fluencia del acero
- f’c = resistencia caracteríastica del hormigón
- As = sección transversal de aceros a tracción en la viga
- Mu = momento solicitante en el punto donde se desea hacer la verificación
En una imagen entenderás mucho mejor varios de estos datos:
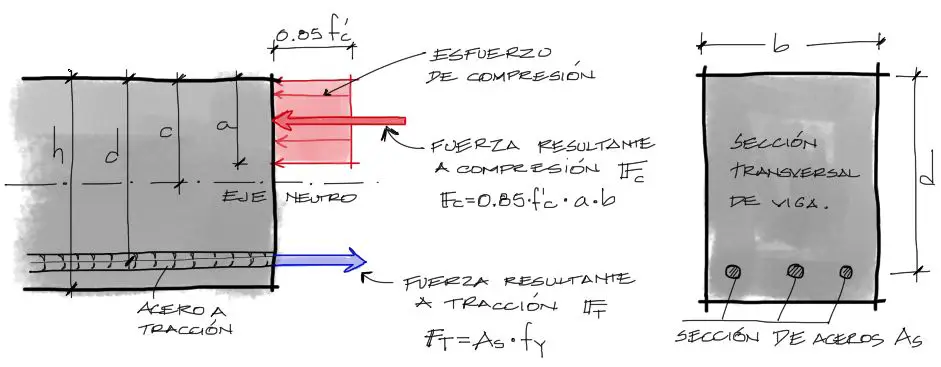
Se supone que se pueden obtener todos los datos mencionados pues estamos en una fase de verificación de la viga, donde todas las dimensiones se conocen porque ya sea que la viga está construida o está representada en planos y conocemos sus dimensiones y refuerzo.
Si por ejemplo conocemos la cantidad de barras de acero y queremos conocer su sección transversal As, podemos consultarlo en tablas que elaboré en el artículo Diámetros de acero y sección transversal.
Otros cálculos adicionales
Con todos los datos anteriores, y antes de comenzar con la deducción de fórmulas de la resistencia de diseño de una viga rectangular, necesitamos unos pequeños cálculos más
Una vez que tengas calculados estos valores, podemos proseguir con el cálculo de revisión de diseño de la viga. Más adelante explicaré con un ejemplo todos los pasos.
Deducción de las fórmulas de momento de diseño
Ahora si, comenzamos con el equilibrio de los esfuerzos internos de la viga para averiguar cuánto resiste la viga de estudio.
Se debe entonces realizar tanto el equilibrio de fuerzas horizontales como de momentos de fuerza dentro de la viga para conocer su resistencia. En la sumatoria de fuerzas horizontales se tiene:

De la misma manera equilibramos los momentos flectores. En este caso el momento de fuerza o par generado por la zona de compresión y tracción, generan el momento resistente que nosotros denominaremos MOMENTO NOMINAL. Este lo obtendremos haciendo pivote justo en el centroide de los esfuerzos de compresión y así anular la expresión de compresión de la ecuación. Se tiene entonces:
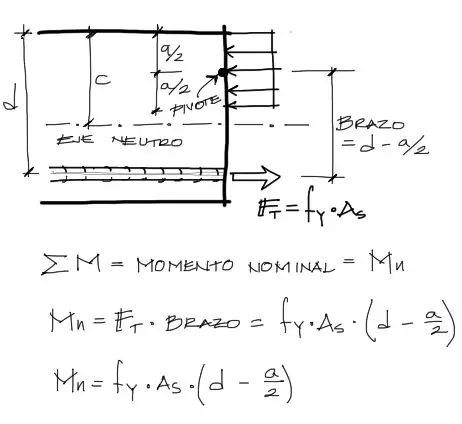
Notarás que de la expresión encontrada acá, el único valor no conocido es “a”, pero este valor lo encontramos en el equilibrio de fuerzas horizontales. Pues reemplazamos entonces el valor de “a” en esta última ecuación, y así obtenemos:
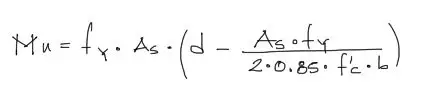
Sin embargo, esta fórmula no lleva aun los factores de seguridad estipulados por la norma ACI para flexión. Aplicando el factor de reducción de resistencias de 0.9 para flexión, la fórmula se convierte en el momento de diseño o momento resistente de diseño a flexión de la viga:
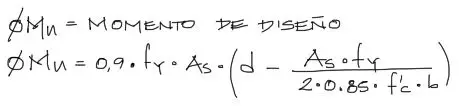
Cómo utilizar la fórmula de øMn
Es importante que leas este apartado!
Si queremos conocer cuanto resiste nuestra viga a flexión, no simplemente debemos aplicar esta fórmula, pues si el acero a tracción con el que contamos en la viga es mayor al acero máximo As-max que mencioné al comienzo del artículo, de nada sirve si es que no se refuerza la zona de compresión de la viga con acero.
Entonces si la viga cuenta con más acero a tracción que As-max, el momento flector resistente de la viga øMn deberá ser igual que øMn-max (que expliqué en el artículo Momento máximo resistente de vigas de hormigón a flexión. Si por el contrario, el acero de nuestra viga “As” es menor a “As-max” entonces podemos utilizar la fórmula expuesta en la demostración.
En resumen:
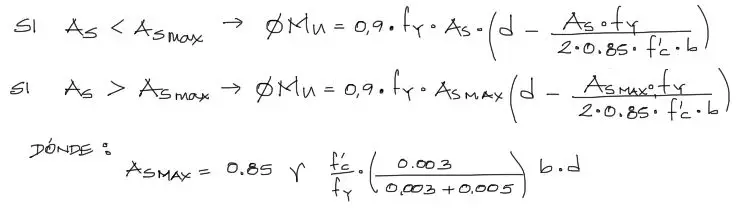
Cabe resaltar como último punto, que a pesar de que uno puede obtener el momento de diseño resistente, cuando éste está calculado a partir de una viga que tiene más acero que As-max, la falla será frágil en la viga, y esto no es muy recomendable.
Ejemplo
Para entender mejor el concepto, te invito a leer el siguiente artículo de Ejemplo de revisión de diseño a flexión de una viga rectangular
autor: Marcelo Pardo
←←← VOLVER A TABLA DE CONTENIDO DE HORMIGÓN ARMADO←←←
→→→ DIAGRAMA DE FLUJO DE DISEÑO A FLEXIÓN DE VIGAS RECTANGULARES →→→



Hola ingeniero buenos días. Quería saber cuando es necesario doble fila de refuerzo a tensión, hay que recalcular el d ¿como hago ese procedimiento? Quedo atento.
Andrés, la doble fila es necesaria cuando en una sola fila no se pueden acomodar todos los aceros y hay que recalcular “d”
si gustas una asesoría para explicarte podemos concretarla si me escribes al +591 698 97074
Hola ingeniero, me surgió una duda, en la parte final donde dice “Entonces si la viga cuenta con más acero a tracción que As-max, el momento flector resistente de la viga øMn deberá ser igual que øMn-max ” no se estará refiriendo que el As será igual a As-max y que cuando es menor se toma el As de la viga. Según la formula que plantea eso es lo que entiendo
Engelbert, buen día. A lo que me referí en ese parrafo es a que la resistencia estará controlada por la compresión del concreto y ya no por la cantidad de barras que tenga la sección a tracción. Cuando se refuerza la sección por encima de As-max ya no interesa cuando acero por demás se coloque. La viga romperá a un momento equivalente a ØMn-max de todas maneras, ya que lo que falla será el concreto, y no el acero.
Ingeniero mil felicitaciones usted es un ejemplo de profesional por compartir todos sus conocimientos para estudiantes y profesionales y nuevamente mis respetos y felicitaciones.
muchas gracias remberto!!
Pingback: Diferencia entre losas llenas y alivianadas
Saludos Ing. Marcelo,
Primero quiero felicitarlo por el gran aporte que da al compartir su conocimiento con tanta claridad. También quería hacer una acotación, en la parte final del documento presentado creo existe un error en el cálculo de As-máx., observo que faltaría ingresar el valor de beta1 en la multiplicación y en el denominador del paréntesis el valor 0.008 debería ser 0.005, para tener la ecuación según el ACI 318-14. De nuevo le agradezco su dedicación, espero siga realizando este trabajo que es de gran ayuda.
Le deseo muchos éxitos.
Tienes toda la razón Alexander! muchas gracias por la observación. La corrijo ahora mismo.
Mil gracias nuevamente!