
Enunciado
Resolver los momentos máximos y mínimos, así como la deflexión máxima de la viga
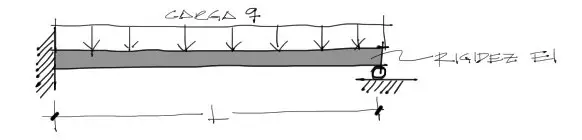
Resolución
Integración de la elástica
Por el Método de la elástica de la viga integramos la ecuación diferencial de cuarto grado, 4 veces.

De esta integración, las incógnitas del problema son las constantes de integración. Estas se obtienen a partir de las condiciones de contorno del problema.
Condiciones de contorno
Las condiciones de contorno se obtienen de los apoyos de la viga. Para empotramientos (a la izquierda) los desplazamientos u y su pendiente du/dx están restringidos, o son iguales a cero. En el extremo derecho, el momento y el desplazamiento vertical son iguales a cero. Notemos que la viga puede girar libremente en el extremo derecho, por tanto la pendiente du/dx no se iguala a cero en este extremo.
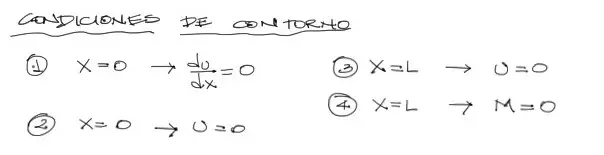
Estas condiciones de contorno deben reemplazarse en las ecuaciones integradas arriba. Si la condición de contorno es de u=0, se reemplaza en la última ecuación. Si la condición es de momento M = EId2u/dx2 = 0, entonces se reemplaza esta condición en la segunda ecuación integrada.
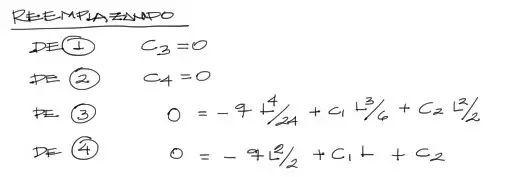
Posteriormente se realiza la resolución y despeje de las constantes C1, C2, C3 y C4, algebraicamente.

Ecuaciones resueltas de la viga
Habiendo encontrado y resuelto las constantes de integración, simplemente se reemplazan estas en cada una de las ecuaciones integradas. Se muestran a continuación las ecuaciones de Momento flector, cortante y deflexión. No se escribe la de pendiente de deflexión por el poco significado físico que representa.
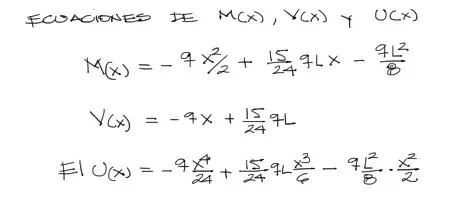
Máximos y mínimos de momento y deflexión
De momento flector
Para poder graficar adecuadamente las ecuaciones de momento flector, cortante y deflexión, necesitamos encontrar los máximos y mínimos de estas ecuaciones.
Para el máximo valor de momento, derivamos la ecuación de momento flector y la igualamos a cero. Posteriormente despejamos “x”. El valor despejado de “x” representa el punto donde el momento flector se hace máximo o mínimo, por definición.

De deflexión
Para la máxima deflexión, el proceso es similar pero un poco más complejo.
De igual manera primero derivamos la ecuación de la deflexión, y la igualamos a cero:
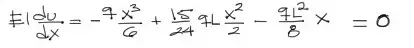
Luego sobre la ecuación derivada debemos despejar y encontrar las raices de “x”. los puntos donde “x” se hace cero representan los lugares donde la deflexión es máxima o mínima. Podemos factorizar “x” y despejar x factorizado. Esto nos indica que una de las soluciones para u máximo se encuentra en x=0.
Las otras dos soluciones o raices de la ecuación la encontramos a partir de la ecuación de segundo grado, que resolvemos mediante la ecuación de segundo grado conocida.

Solo la solución que está entre 0 y L es válida. La otra solución no nos sirve por encontrarse fuera del rango.
Reemplazamos el valor de “x” obtenido dentro de la ecuación de la deflexión para averiguar el valor de la deflexión máxima. En este punto ya no conservamos fracciones y resolvemos la ecuación con decimales.

Graficación
A partir de todos los datos obtenidos, ya se pueden graficar todas las ecuaciones:
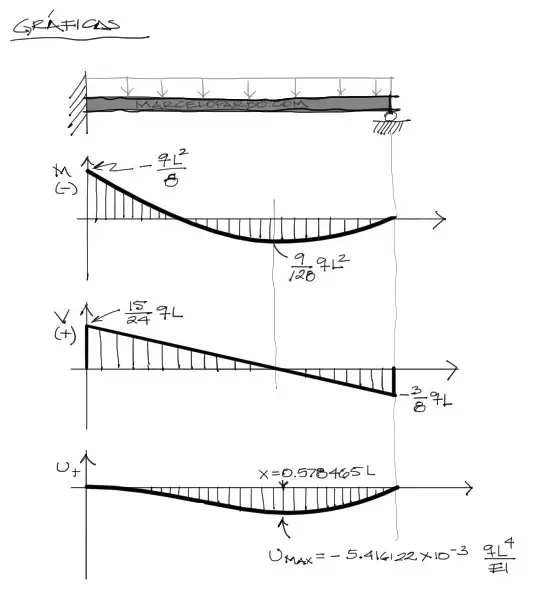
autor: Marcelo Pardo

