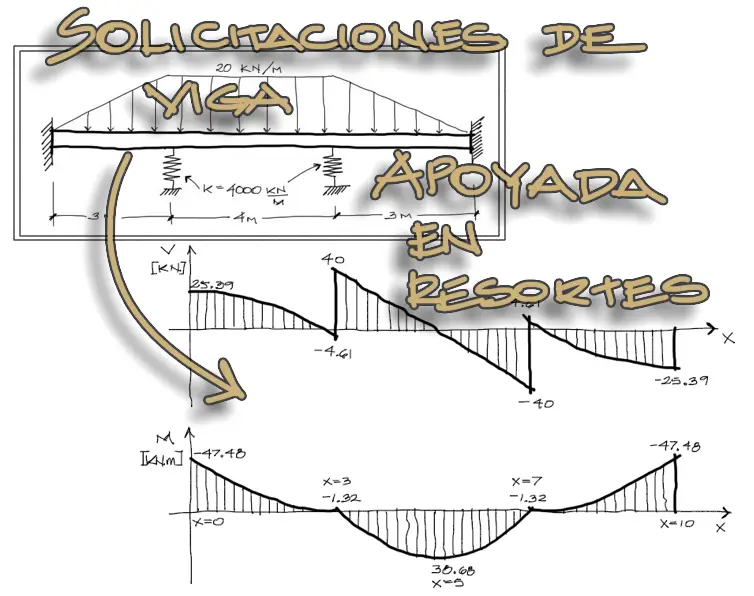
Pasos previos
Este artículo es la continuación de un anterior análisis donde se hizo todo el tratamiento matricial por el método de rigidez para encontrar los desplazamientos de los nudos de la viga del gráfico.
Para ver esta primera parte puedes dirigirte al enlace VIGA HIPERESTÁTICA SOBRE APOYOS ELÁSTICOS – DESPLAZAMIENTOS Y REACCIONES.
Si ya leiste el anterior artículo, ahora debemos aplicar una serie de pasos que no son parte del método de elementos finitos ni de rigidez precisamente, sino nacen de la deducción elástica de un tramo de viga sometido a deformaciones arbitrarias en los extremos.
La teoría de estos pasos la encuentras en el enlace TEORÍA DE CORTANTES Y MOMENTOS A PARTIR DE LOS DESPLAZAMIENTOS EN NUDOS.
Datos necesarios
Para la resolución de este problema solo se necesitan los datos de rigidez de la viga, los desplazamientos de los nudos y los valores de la carga. O sea:
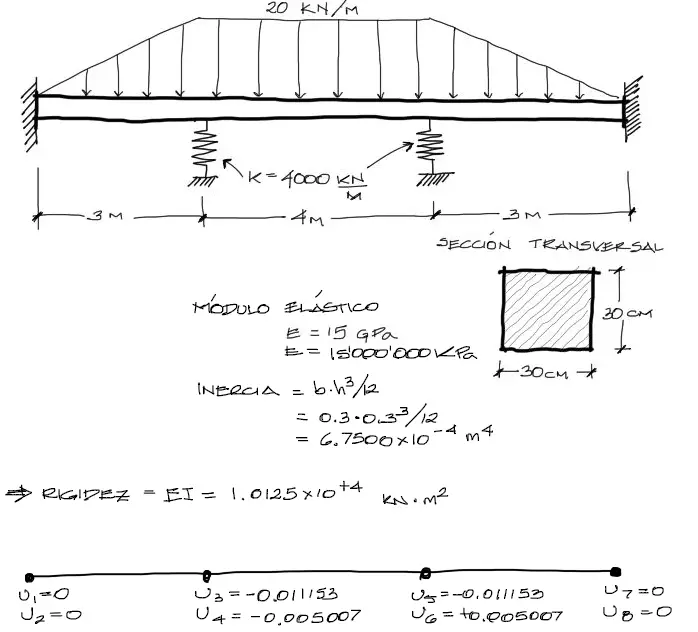
Solicitaciones en Tramo 1
Con todas las herramientas estudiadas, podemos abrodar el problema. Analizaremos el primer tramo a todo detalle, y los otros tramos serán muy similares.
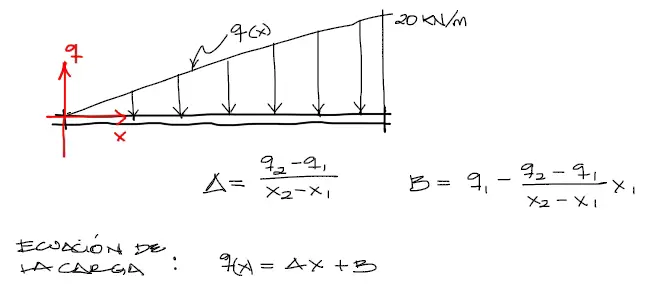
Ecuación de la carga de Tramo 1
El primer paso en todo este análisis es conocer la ecuación que proyecta la carga variable a lo largo del primer tramo. Para eso imaginamos el plano coordenado con origen en el extremo izquierdo de la viga. Luego obtenemos la ecuación a partir de las fórmulas de la teoría.
Reemplazando los datos anteriores, tenemos los siguientes valores de A y B:
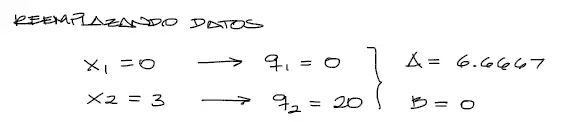
Constantes de integración de tramo 1
La parte más importante del cálculo de solicitaciones consiste en resolver el sistema de ecuaciones publicado en la teoría, que se vuelve a mostrar a continuación:
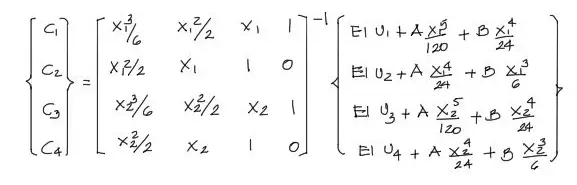
De todos los datos mostrados, ya conocemos las coordenadas del tramo, X1 = 0 y X2=3m. También conocemos A y B. Finalmente los datos de U1 U2 U3 U4 corresponden a los desplazamientos y giros de los nudos 1 y 2 respectivamente.

Acto seguido se resuelve el sistema matricial quedando:
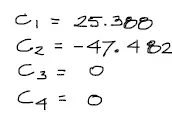
Graficación de Solicitaciones del tramo 1
Las constantes anteriores encontradas son parte de la ecuación de la elástica de la viga ya integrada. Tiene la siguiente forma:
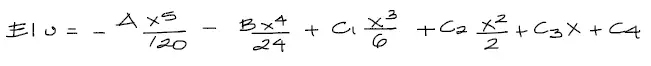
Si derivamos la ecuación mostrada dos veces obtenemos el momento flector, y si la derivamos respecto de X una vez más obtenemos el cortante.
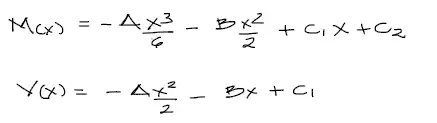
Por tanto reemplazando los datos ya encontrados, tenemos las ecuaciones de momento y cortante para el tramo 1
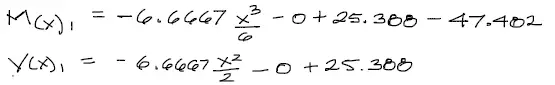
Solicitaciones del tramo 2
el procedimiento es es exactamente igual al del tramo 1. Solo se debe tener cuidado de dos cosas:
- Las coordenadas X1 y X2 se deben tomar siempre desde el sistema coordenado global, con origen en el extremo izquierdo de la viga.
- Los desplazamientos locales u1, u2, u3, u4 de del tramo en análisis correponden a los desplazamientos globales del tramo que en general tendrán una numeración diferente. Por ejemplo el tramo 2 tiene los desplazamientos U3 U4 U5 U6, que para propósitos de la resolución del sistema de ecuaciones se convertirán temporalmente en u1 u2 u3 u4 “locales”
O sea, los datos de ingreso al sistema matricial de constantes para el tramo 2 serán:

Luego las ecuaciones de momentos y cortantes para el tramo 2 son:
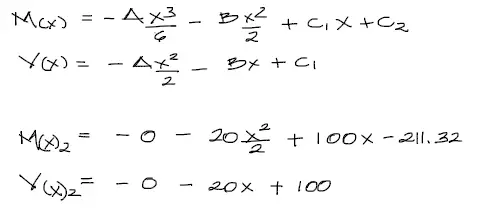
Solicitaciones del tramo 3
Las mismas consideraciones de anteriores tramos se aplican para este tramo. Entonces los datos y resultado de constantes, así como momentos flectores y cortante para el tercer tramo son:

Graficación
Son tres tramos de análisis con tres tramos de graficación según los siguientes límites:
– Tramo 1: x entre [0 y 3]
– Tramo 2: x entre [3 y 7]
– Tramo 3: x entre [7 y 10]
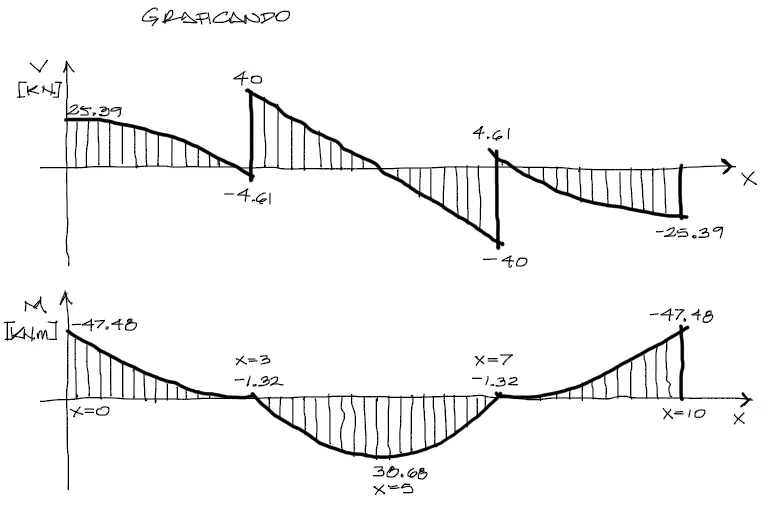
De la misma manera se puede graficar la deflexión de la viga U despejando la variable U de la rigidez EI (pasándola a dividir al miembro derecho). Eso lo dejo como ejercicio al lector.
←←← VOLVER A: DESPLAZAMIENTOS Y REACCIONES DE VIGA APOYADA EN RESORTES ←←←
autor: Marcelo Pardo


Magnífico. Excelente. Genial.