Pasos previos
Continuación del ejercicio: RESOLUCIÓN DE VIGA CON ARTICULACIÓN, POR EL MÉTODO DE RIGIDEZ.
En el anterior artículo habíamos resuelto tanto los desplazamientos y reacciones en los apoyos de la siguiente viga:
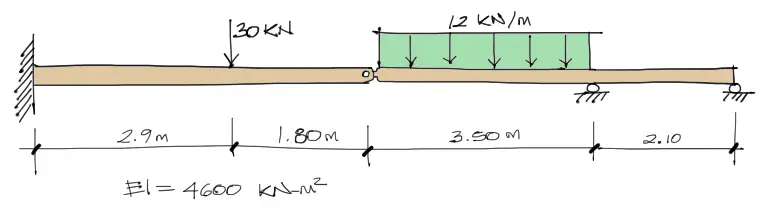
Son precisamente los siguientes desplazamientos encontrados:
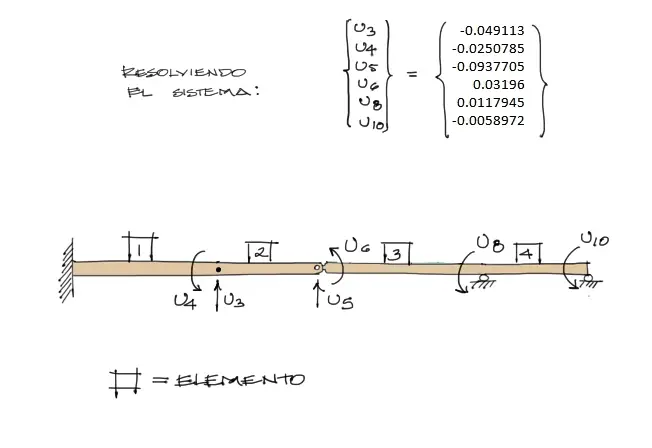
Cabe resaltar que la imposición de articulaciones en el método de rigidez se realiza a los elementos y no a los nudos en sí. Por tanto en este ejercicio se impuso una articulación solo al nudo derecho del elemento 2. El elemento 3 cuenta con todos sus grados de libertad. (ver artículo anterior).
A la vez encontramos las reacciones del sistema:
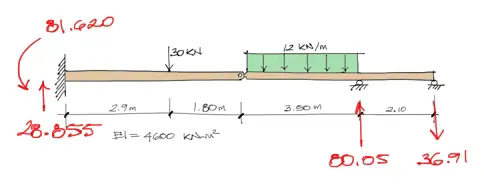
Solicitaciones de la viga
Solicitaciones en los extremos de cada tramo
Lo que corresponde en este apartado es encontar las articulaciones de los 4 tramos bajo una metodología que permita hacer el cálculo automático.
Para eso debemos recurrir a las matrices de rigidez de cada elemento y encontrar las solicitaciones de los extremos de cada barra, de la siguiente manera.
Se puede conformar un sistema de ecuaciones a partir de la matriz de rigidez de cada elemento y sus desplazamientos igualados a las fuerzas que actuan en el elemento. En fórmula se tiene:
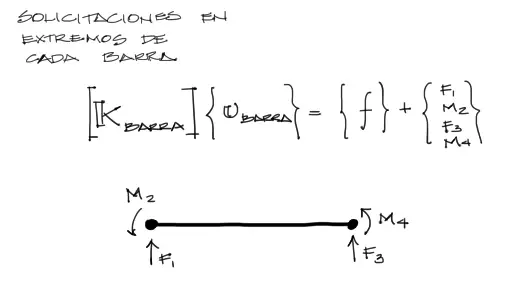
En el caso de la barra articulada (elemento 2) el sistema que se forma es similar, pero sin el grado de libertad de giro del lado derecho (que se eliminó para generar la articulación):
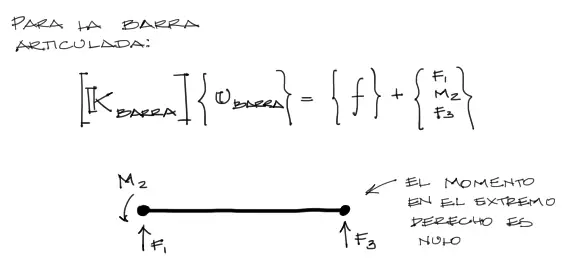
Realizamos entonces el reemplazo con los valores numéricos para cada elemento donde las únicas incógnitas son las solicitaciones de fuerza y momento de fuerza para los extremos de cada barra. Los desplazamientos se reemplazan a partir del vector U encontrado al final del anterior artículo.
Al elemento 1 le corresponden los desplazamientos u1, u2, u3, y u4.
Al elemento 2 le corresponden los desplazamientos u3, u4, u5.
Al elemento 3, u5, u6, u7, u8.
Al elemento 4, u7, u8, u9, u10.
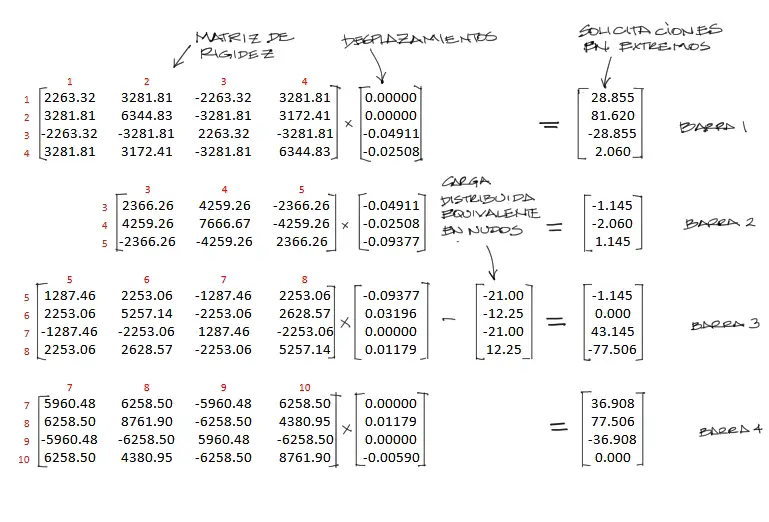
Se debe puntualizar que cuando el elemento contiene una carga distribuida, se debe incluir en la ecuación de equilibrio el vector de cargas equivalentes en los nudos. Este es el caso del elemento 3, cuyo vector de cargas equivalentes se calculó en el artículo anterior.
Solicitaciones en el interior de cada elemento
Una vez que se tienen las solicitaciones en los extremos de cada tramo, junto con los datos de las coordenadas de los nudos del tramo y la ecuación de la carga, se puede conseguir de manera relativamente sencilla la ecuación de diagrama de momento flector para ese tramo.
Para eso, recurriremos a la ecuación de la elástica de la viga, que integrada dos veces nos proporciona la ecuación de momento flector. En el caso de no existir cargas distribuidas en el tramo, la función que describe la forma de la carga distribuida q(x) será igual a cero.

En la imagen vemos que la ecuación de la elástica de la viga se integra dos veces y se generan dos constantes de integración que son la incógnita de la ecuación. Estas constantes C1 y C2 se resuelven con condiciones de contorno del tramo. Como se conocen los momentos flectores en los extremos y las coordendas de los extremos, reemplazamos estos datos en la ecuación de momento flector M(x). Se forma un sistema de dos ecuaciones con dos incógnitas. Encontrados C1 y C2, se tiene la ecuación de momento y de cortante para cada tramo.
Ecuación de momento flector para el tramo 1
Para el tramo 1, la carga distribuida es nula, por tanto la ecuación de momento es como la mostrada en el anterior subtítulo. Los momentos de los extremos del tramo 1 se muestran a continuación:
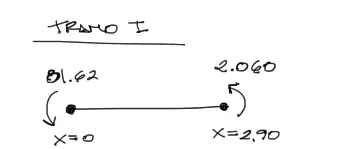
Se debe tomar en cuenta que en la convención de signos de ecuaciones de momento flector para la graficación, el momento que tracciona las fibras inferiores es positivo. En cambio los resultados obtenidos por el método de rigidez tienen la convención de momento positivo antihorario. esto se ve en la siguiente imagen:
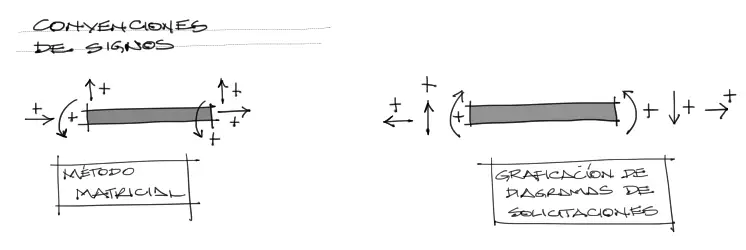
Por tanto en el reemplazo de los momentos dentro de las ecuaciones de M(x) el momento de la izquierda entra como negativo, pues comprime las fibras inferiores. Notemos que este momento de 81.62 es positivo en los resultados del método de rigidez.

Se reemplazan además las coordenadas de X para cada extremo y se resuelve el sistema de ecuaciones conociendo así C1 y C2. Con esto ya se pueden escribir las ecuaciones de momento flector y cortante para el tramo 1.

Ecuaciones M y V para el tramo 2
El procedimiento del tramo 2 es completamente igual al del tramo 1, con la peculiaridad de que en este tramo articulado, el momento flector de la derecha no existe o es igual a cero.
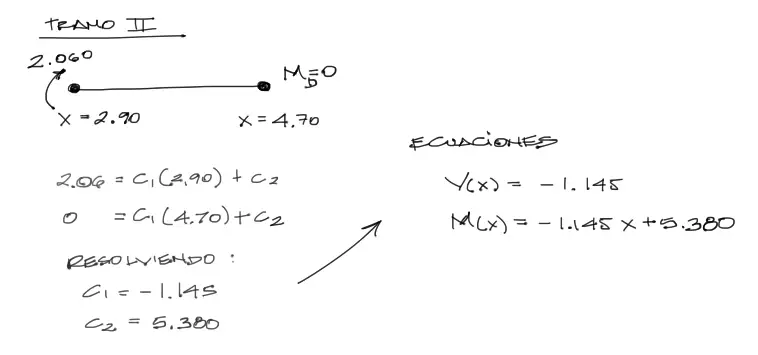
Ecuaciones de momento y cortante para el tercer tramo
El tercer tramo cuenta con una carga distribuida constante a lo largo de toda su longitud. por tanto q(x) en la ecuación de la elástica es 12 KN/m. Se reemplaza este valor en la elástica y se integra dos veces de la manera ya mencionada. Luego se reemplazan los momentos de los extremos, las coordenadas y se procede a encontrar C1 y C2:

Se puede ver entonces que el procedimiento es mecánico para todos los tramos.
M y V de Tramo 4
De igual manera que con el tramo 1, se tiene:
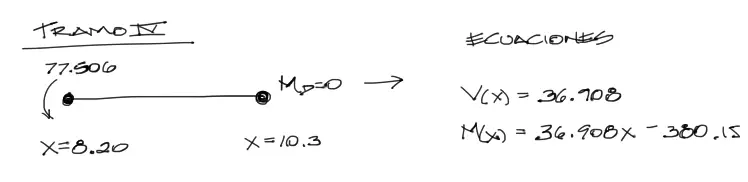
Graficación
Se tienen las ecuaciones de momento flector para los 4 tramos. Si los graficamos uno tras otro se obtiene:
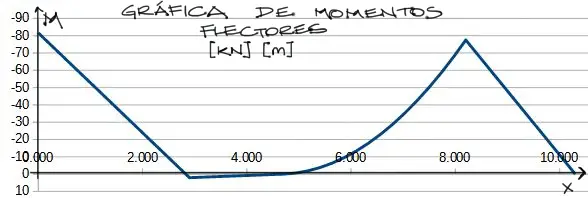
el mismo ejercicio puede hacerse para el diagrama de cortante.
autor: Marcelo Pardo