Como leer el índice

El método de elementos finitos y método de rigidez coinciden en las fórmulas finales que se utilizan en estas publicaciones, así que no se hace una distinción explícita entre ambos métodos.

Los temas numerados son desplegables. Al desplegar cada menú, existen los enlaces de los artículos. A la derecha de cada artículo existen íconos que tienen el siguiente significado:
Artículo escrito:
Video de Youtube:
Vídeo de youtube de zona de miembros:
Programa en Línea:
Curso de pago:
Diagrama de flujo:

→ CONCEPTOS

– Introducción a los métodos numéricos. ¿Para qué sirven?
– Introducción al método de elementos finitos
– Diferencia entre el método matricial de rigidez y el método de elementos finitos
– ¿Qué son Grados de Libertad?

→ ELEMENTO DE BARRA EN 1-D

– Teoría – Elemento de barra en una dimensión. Deducción de la matriz de rigidez
– Vídeo de Elementos de barra con un grado de libertad

→ CERCHAS

TEORÍA
– Demostración de matriz de rigidez de cercha en 2 Dimensiones
– Demostración de matriz de rigidez de elemento de cercha en 3 dimensiones
– Pasos para el cálculo de cerchas por el método de rigidez
EJEMPLOS
– 1er ejemplo de cercha en 2D por método Matricial
– 1er Ejemplo de cercha 2D – Continuación – Solicitaciones
– 2do Ejemplo de Cercha 2D. Desplazamientos, reacciones, solicitaciones
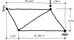
– Cercha en 3D. Desplazamientos, reacciones, solicitaciones

→ VIGAS

TEORÍA
– Fórmula de matriz de rigidez de viga
– Demostración de la matriz de rigidez de viga
– Teoría de Momentos flectores y cortantes a partir de deflexiones en los extremos
– Matriz de rigidez de elemento de viga articulada en un extremo y en dos extremos
EJEMPLOS
– Ejemplo de resolución de viga hiperestática (Primera Parte)
– Ejemplo de viga hiperestática (2da parte) – diagramas de Momentos y Cortantes
– Viga sobre apoyos elásticos. Ejemplo
– Solicitaciones en viga apoyada en resortes (Continuación)
– Ejemplo de viga hiperestática con articulación (Parte 1 – desplazamientos)
– Ejemplo de viga hiperestática con articulación (Parte 2 – Solicitaciones)
– Ejemplo de viga apoyada sobre lecho elástico (Resolución con excel) – PARTE I
– Ejemplo de viga apoyada sobre lecho elástico (Resolución con excel) – PARTE II
CURSOS
– Curso de Programación en OCTAVE o MATLAB de resolución de vigas por el método de rigidez

→ Curso de programación de Vigas por método de rigidez con PYTHON

– 01 Curso – Viga por Rigidez con PYTHON – Ingreso de datos
– 02 Curso – Viga por Rigidez con PYTHON – Ingreso de Datos
– 03 Curso – Viga por Rigidez con PYTHON – Matrices rigidez elementos
– 04 Curso – Viga por Rigidez por PYTHON – Ensamblaje de matriz de rigidez de la estructura
– 05 Curso – Viga por Rigidez por PYTHON – Vector de cargas Puntuales de viga en Python
– 06 Curso – Viga por Rigidez por PYTHON – Vector de cargas distribuidas de viga en Python
– 07 Curso – Viga por Rigidez por PYTHON – Vectores de Grados de libertad
– 08 Curso – Viga por Rigidez con PYTHON – Desplazamientos y reacciones en vigas
– 09 Curso – Viga por Rigidez con PYTHON – Graficación de diagramas de momentos y deformaciones en programa de viga con Python
– 10 Curso – Viga por Rigidez con PYTHON – Gráfica de viga, Cortante, Momento y Deflexión
– 11 Curso – Viga por Rigidez con PYTHON – Gráfica de cargas puntuales
– 12 Curso – Viga por Rigidez con PYTHON – Gráfica de cargas distribuidas
– 13 Curso – Viga por Rigidez con PYTHON – Dibujo de apoyos
– 14 Curso – Viga por Rigidez con PYTHON – Valores numéricos de diagramas M y V

→ PÓRTICOS EN DOS DIMENSIONES

TEORÍA
– Matriz de Rigidez de Pórtico en 2 dimensiones
– Vector de cargas puntuales para pórticos en 2 dimensiones
– Vector de cargas distribuidas equivalentes en pórticos en 2 dimensiones
– POSTPROCESO: diagramas de momento flector, cortante y axial a partir de desplazamientos de nudos
– Resortes en pórticos en 2 dimensiones
– Matriz de rigidez de elementos articulados en pórticos
– Solicitaciones en elementos de pórtico (incluso con articulaciones)
PROGRAMA
– MatrixPro – PROGRAMA DE PÓRTICOS EN 2 DIMENSIONES gratuito
– MatrixPro – Ejemplo 1 de pórtico
-MatrixPro – Ejemplo 2 de viga sobre lecho elástico
EJEMPLOS
– Pórtico con cargas puntuales – Parte 1
– Pórtico con cargas puntuales – Parte 2 – SOLICITACIONES
– Pórtico en 2D con cargas distribuidas – Parte 1 – Matriz de rigidez
– Pórtico en 2D con cargas distribuidas – Parte 2 – Análisis de cargas
– Pórtico en 2D con cargas distribuidas – Parte 3 – Solución del sistema
– Pórticos en 2D con cargas distribuidas – Parte 4 – Diagramas de momento, axial y cortante
– Pórtico con desplazamiento impuesto. Desplazamientos, reacciones y Momentos flectores
– Pórtico con apoyo de resortes. Cálculo de reacciones de apoyos y desplazamientos de nudos
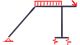
– Pórtico con apoyo de resortes. Corrección de pequeño error y comprobación con software
– Resolución de Pórtico con articulaciones – PARTE I
– Resolución de Pórtico con articulaciones – PARTE II
– Resolución de Pórtico con articulaciones – PARTE III
CURSOS
– Curso de Programación de pórticos en Matlab y GNU Octave

→ PÓRTICOS EN 3 DIMENSIONES

TEORÍA
– Matriz de rigidez de Elemento de barra de pórtico en 3D
– Coordenadas locales y globales de elemento de barra en pórtico en 3D
– Programando la rotación de la barra de pórtico en 3D
EJEMPLOS
– Voladizo circular (parte1) – Matrices de rigidez local
– Voladizo circular (parte2) – Matrices de rigidez global de toda la estructura
– Voladizo circular (parte3) – Vector de cargas

→ ARCOS

TEORÍA
EJEMPLOS
– Arco parabólico. Parte 1: Matrices de rigidez
– Arco parabólico. Parte 2: Desplazamientos de nudos y reacciones
– Arco parabólico. Parte 3: Solicitaciones en elementos

→ TEMAS DIVERSOS

– Cómo generar mallas de elementos finitos con GMSH

→ TABLAS ÚTILES (MEP, INERCIAS, etc)

– Tabla de cargas equivalentes en los extremos a partir de cargas distribuidas (M.E.P.)